[게임 수학] #6 | 삼각함수(2) : 각의 측정법

인프런 <게임 엔진을 지탱하는 게임 수학, 이득우 교수님> 강의를 보며 공부한 글입니다.

 

 

1. 각의 측정

각도법 (Degree)

원을 360개로 균일하게 나누어 표현하는 방법입니다. 일상에서 흔히 사용하는 방법이죠. 왜 360인가에 대해서는 약수가 많이 나오는 수이기 때문에 원을 쪼개서 계산할 때 유용하다고 합니다.

 

하지만 이러한 각도법보다는 원의 호의 길이를 이용해 각도를 표시하는 호도법(Radian)이 삼각함수에 더 적합합니다. 삼각함수의 미적분을 더 편리하게 적용할 수 있기 때문이죠. 그렇다면, 우선 호도법이 뭔지부터 알아봅시다.

 

 

호도법 (Radian)

반지름이 1인 반원을 생각해봅시다.

 

반지름 길이가 1인 반원

 

 

위와 같이 존재하는 반지름이 1인 반원의 왼쪽 좌표를 원점으로 옮겨봅시다.

 

왼쪽 좌표를 원점으로 옮긴 모습

 

 

이 때, 이 원호를 오른쪽으로 쫘악 펼쳐봅시다. 마치 오른쪽 끝이 실이라고 생각하고 쭉 당겨 펼치는 것처럼요. 그러면 다음과 같은 모양이 됩니다.

 

원호를 쫙 펼친 모습

 

이렇게 하면 기존에 알고 있던 반지름 크기 1과 비교했을 때, 원호의 길이가 몇 배만큼 늘어났는지 측정할 수 있습니다 이 때 무리수가 나오게 되는데, 이것이 바로 원주율 \(\pi\)가 됩니다.

 

의미를 좀 더 확장해서 반지름이 \(r\) 인 상황이라면, 반원의 둘레는 \(\pi r\) 이 되겠지요. 그래서 원의 둘레 공식이 \(2\pi r\) 이구나라고, 이 글을 작성하며 그런 생각이 들었습니다. 아무튼, 이 상황에서 다시 반대로 되감아보도록 합시다.

 

 

 

부채꼴을 형성하는 모든 변의 길이가 1이 되었을 때, 각의 값을 기본 단위로 "1 래디안"이라 부른다.

 

위와 같이 \(\pi\) 길이 중에서 길이가 1인 만큼만 거꾸로 되감는거죠. 이 때 나오는 각(ɵ)의 값 역시 무리수가 됩니다. 이것을 호도법의 단위인 래디안(\(rad\))이라고 부릅니다. 다시 말해, 반지름과 호의 길이가 1로 같아진 상태일 때, 이 상황에서의 각도를 1 래디안이라고 부르는 것이죠.

 

만약 \(\pi\)만큼 되감으면 180°에 해당하는 반원이 채워지게 될 겁니다.

왜냐하면 180°라는 것은 1 래디안을 \(\pi\) 배만큼 회전시킨 것과 같기 때문이죠.

 

$$ 180 = \pi(rad) $$

$$ 1 = \frac{\pi}{180}(rad) $$

$$ 1(rad) = \frac{180}{\pi} $$

 

자주 사용되는 각도에 대응하는 호도값

 

$$ 90=\frac{\pi}{2}(rad) $$
$$ 60=\frac{\pi}{3}(rad) $$
$$ 45=\frac{\pi}{4}(rad) $$
$$ 120=\frac{2\pi}{3}(rad) $$

 

 

그렇다면, 왜 호도법에 대해 배우는 건가?

실제 수학에서 사용하는 것과 컴퓨터에서 삼각함수를 다룰 때는 모두 호도법을 기준으로 전개하기 때문입니다. 이런 내용들은 주로 벡터의 회전(Rotation of Vector)에서 응용하여 사용할 수 있습니다.

 

---

2. 벡터의 회전 (Rotation of Vector)

어떤 물체를 일정 각도만큼 회전시킬 때 삼각함수를 많이 사용하게 됩니다. 회전하기 전, 실 벡터공간 \(\mathbb{R}^2\) 의 임의의 원소를 \((x, y)\) 라고 해봅시다. 이 \((x, y)\) 는 표준 기저 벡터 \(e_1, e_2\) 를 선형 조합하여 다음과 같이 분해하여 생각할 수 있습니다.

 

$$ (x,y)=x(1,0)+y(0,1) $$

 

이 때, 외부의 힘이나 어떠한 요인에 의해서 공간이 변형됐다고 가정해봅시다. 공간의 일부만 변환된 것이 아니라 공간 전체가 변환되어 버린 것이죠.

하지만 벡터 공간은 무한대의 영역입니다. 무한대에 존재하는 모든 벡터들을 하나씩 다 변환시킬 수는 없는 노릇입니다. 이런 상황인데, 공간 전체가 변환됐다는 컨셉을 어떻게 잡을 수 있을까요?

 

 

결국, 이 공간의 모든 요소들은 벡터 공간을 이루는 두 개의 기저 벡터를 조합해서 만든 것이기 때문에, 이 기저 벡터를 변화시키면무한대의 벡터 요소들을 일일히 추적하지 않아도 대략적으로 어떤 식으로 변화되는지를 유추할 수 있게 됩니다. 마치 집의 주춧돌이 변하면, 집의 모양이 변하는 것처럼요.

 

 

표준 기저 벡터로 이루어진 벡터 공간 \(\mathbb{R}^2\) 의 두 기저 벡터가 새로운 값으로 변한다면, 벡터 공간의 원소 \((x, y)\) 는 새로운 두 기저 벡터에 각각 \(x\)와 \(y\) 를 곱한 벡터에 대응됩니다.

 

이 때, 새로운 두 기저 벡터가 크기가 1, 직교하는 상태와 현재 방향을 유지하면서 변형하는 것을 회전 변환이라고 합니다. 각 \(\theta\) 만큼 발생한 회전 변환을 통해 임의의 벡터가 어떻게 변화되는지를 한 번 살펴보죠.

 

 

회전 변환

 

$$ e_1\mapsto (cos\theta, sin\theta) $$
$$ e_2\mapsto (-sin\theta, cos\theta) $$

 

 

표준 기저 벡터 \(e_1 (1, 0)\)이 각 \(\theta\)만큼 회전을 했을 때, \((cos\theta, sin\theta)\)로 변환됩니다.

표준 기저 벡터 \(e_2 (0, 1)\)이 각 \(\theta\)만큼 회전을 했을 때, \((-sin\theta, cos\theta)\)로 변환됩니다.

 

그렇다면, 이렇게 각각 변환된 \(e_1, e_2\) 기저 벡터에다가 \((x, y)\)를 곱해주면, 원 공간에서 \((x, y)\)라는 이 벡터가 각 \(\theta\)만큼 회전한 새롭게 변화된 공간에서 어떠한 값에 대응되는지를 알아낼 수가 있습니다.

 

$$ v=(x,y)=x\cdot e_1+y\cdot e_2 $$

$$ v'=x\cdot (cos\theta, sin\theta)+y\cdot (-sin\theta, cos\theta) $$

$$ =(xcos\theta-ysin\theta, xsin\theta+ycos\theta) $$

 

 

\((x, y)\) 좌표가 새롭게 회전 변환된 공간의 \((xcos\theta-ysin\theta, xsin\theta+ycos\theta)\)라는 좌표에 대응된다는 것을 볼 수 있는 식이었습니다.

 

 

---

3. 삼각함수의 역함수 (Inverse trigonometric functions)

반대로 공역이 정의역이 되고, 정의역이 공역이 되는 뒤집은 관계를 살펴봅시다. 역함수가 존재하기 위해서는 해당 함수가 전단사 함수여야 합니다. 공역과 치역이 같고 일대일 대응 함수여야 한다는 것이죠.

 

하지만 사인, 코사인, 탄젠트 함수는 일대일 대응이 아니기 때문에 단사 함수가 아닙니다.

따라서, 의도적으로 전단사 함수로 만들기 위해 정의역의 값을 제한시킬 겁니다. 이렇게 한다면 역함수가 존재하겠죠.

 

사인 함수와 코사인 함수 그래프

탄젠트 함수 그래프

 

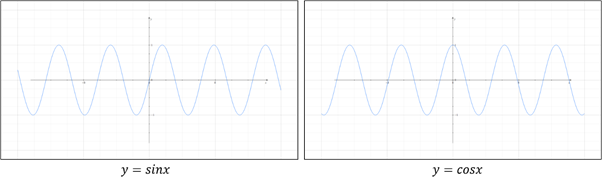
각 삼각함수가 전단사 함수가 될 수 있는 정의역 구간을 나누자면 다음과 같습니다.

• 사인(sin) 함수  :  \([-\frac{\pi}{2}, \frac{\pi}{2}]\)
• 코사인(cos) 함수  :  \([0, \pi]\)
• 탄젠트(tan) 함수  :  \((-\frac{\pi}{2}, \frac{\pi}{2})\)

 

이렇게 제한한 영역을 주욧값(principal value)라고 부릅니다. 그리고, 위의 범위에서 정의한 역함수를 각각 아크사인(arcsin), 아크코사인(arccos), 아크탄젠트(arctan) 함수라고 부르죠. 역함수의 기호는 다음과 같이 표현합니다.

 

$$ y = sin(x) $$

$$ y = sin^{-1}(x) $$

$$ y = arcsin(x) $$

 

 

삼각함수의 역함수 문제점

arcsin

arccos

arctan

 

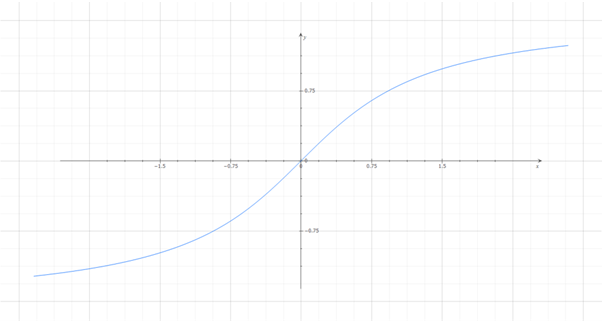
역함수가 다루는 각의 범위는 다음과 같습니다.

• 아크사인 함수의 치역  :  \([-\frac{\pi}{2}, \frac{\pi}{2}]\)
• 아크코사인 함수의 치역  :  \([0, \pi]\)
• 아크탄젠트 함수의 치역  :  \((-\frac{\pi}{2}, \frac{\pi}{2})\)

 

 

 

역함수를 통해 어떤 값을 가지고 있을 때, 거기에 대응되는 각도를 알 수가 있습니다.

다만, 위 그림처럼 3사분면에 해당하는 값을 알 수는 없습니다. 전단사 함수를 만족해야 하기 때문에 일정 구간을 버렸고, 거기에 해당하는 영역이기 때문이죠. 여기에 대한 값에 대한 각도는 어떻게 알아낼 수 있을까요?

 

 

아크탄젠트 함수의 활용

전단사 함수를 만족하기 위해 버렸던 구간 값에 대한 각도를 알아내기 위해, 아크탄젠트 함수를 활용할 수 있습니다. 아크탄젠트 함수는 밑변과 높이가 주어졌을 때, 거기에 대한 각도를 얻어낼 수 있죠.

 

두 삼각형은 다른 삼각형이고 다른 각을 가지지만, 탄젠트 값은 동일하다.

 

실제로 \(\frac{높이}{밑변}\)이라는 값이 양수가 나오려면 위 그림처럼 \(x, y\) 모두 양수인 경우도 있지만,

음수인 경우에도 \(x, y\)가 같은 부호를 가지기 때문에 양수의 값이 나오게 됩니다.

 

이 말은 아크탄젠트 함수를 통해 어떤 값을 기반으로 각도를 알아내려고 하면, 두 가지 경우가 존재할 수 있다는 겁니다. 만약 \(x\)나 \(y\)가 음수라는 정보 또한 주게 된다면요?

 

값은 양수인데, 하나의 값(x or y)이 음수라면 1사분면에 있는 삼각형이 아니라 3사분면에 있는 삼각형을 뜻합니다. 따라서, 부호 정보까지 추가로 전달해주면 위의 두 삼각형은 구분할 수 있게 됩니다. 이것에 대한 아크탄젠트 함수로 인자를 두 개 받는 \(atan2(y, x)\)가 많이 사용됩니다.

 

따라서, 어떤 벡터의 각을 알고 싶다면, 탄젠트의 역함수 \(atan2\)를 사용하여 알아낼 수 있습니다.

 

 

---

4. 극 좌표계 (Polar Coordinate)

벡터 공간 평면에 속한 어떤 임의의 좌표를 x축의 값과 y축의 값을 조합하여 표현한 좌표계가 데카르트 좌표계였습니다. 극 좌표계는 벡터 공간 평면이 원으로 구성되어 있다는 생각에서 출발합니다. 무수히 많은 원들로요. 그 많은 원들이 가지고 있는 값을 반지름 \(r\) 로 표시하고, 해당 원호 위의 한 점을 각 \(\theta\) 으로 표현합니다.

 

 

 

즉, 평면의 한 벡터의 값을 어떤 원이 그리는 반지름(r)과 이루는 각 \(\theta\)로 표현하는 방식인 셈이지요. 이런 극 좌표계는 반지름 크기에 비례해서 중심에서 멀어질 수록 회전을 더 많이 주고 싶은 경우에 활용이 가능합니다. 이런 극 좌표계와 데카르트 좌표계는 서로 변환이 가능합니다.

 

 

데카르트 좌표계 →  극 좌표계 변환

회전을 좀 더 편하게 하기 위해, 극 좌표계로 변환하여 적용할 수도 있습니다.

• \( r = \sqrt{x^2 + y^2}\)
• \( \theta = atan2(y, x)\)

 

$$ r=\sqrt{x^2+y^2}=size(v) $$

$$ \theta = atan2(y, x) $$

 

 

극 좌표계 →  데카르트 좌표계 변환

호도법에서 봤던 개념을 그대로 이용할 수 있습니다.

 

$$ x=r\cdot cos\theta $$
$$ y=r\cdot sin\theta $$