2022. 7. 21. 17:21ㆍComputer Sciences/Game Mathemathics
인프런 <게임 엔진을 지탱하는 게임 수학> 이득우 교수님 강의를 보며 공부한 글입니다.
1. 벡터의 생성(Span) 시스템
벡터가 가지고 있는 벡터와 벡터의 덧셈, 벡터와 스칼라의 곱셈 이 두 가지 연산을 이용하여 새로운 벡터를 생성해내는 시스템을 말합니다. 수의 시스템에서 수와 수의 이항 연산을 통해 새로운 수를 생성해내는 시스템과 비슷하다고 볼 수 있죠. 이렇게 생성하는 시스템을 선형 조합(Linear Combination)이라고 하고, 수학에서는 이렇게 새로운 벡터를 생성하는 것을 Span 한다고 표현합니다.
선형 조합(Linear Combination)이란?
벡터의 기본 연산을 사용하여 새로운 벡터를 생성하는 수식을 말합니다.
$$ v'=a_1 v_1+a_2 v_2+a_3 v_3+⋯+a_n v_n $$
선형 의존과 선형 독립의 수학적 정의
같은 수의 성분을 가진 \(n\) 개의 벡터 \(v_1, \ v_2, \ , ..., v_n\) 에 대하여, 이들의 벡터 선형 조합인 다음 식이 있다고 가정합시다.
$$ a_1 v_1+a_2 v_2+a_3 v_3+...+a_n v_n=\vec{0} $$
- 위 식의 계수들(\(a_i\))들 중 0이 아닌 계수가 존재하면, 수식 내 벡터들은 선형 의존(Linear dependent)이라고 합니다.
- 위 식의 모든 계수(\(a_i\))들의 값이 0이라면, 수식 내 벡터들은 선형 독립(Linear independent)이라고 합니다.
그래서 이게 어떤 의미인데?
예시 문제를 보며 알아봅시다.
(1, 1)과 (2, 2)는 선형 의존인가? 선형 독립인가?
$$ a_1(1,1)+a_2(2,2)=\vec{0} $$
여기서 \(a_1, a_2\)는 스칼라(scalar)를 의미합니다. 위의 식에서 \(a_1 = 2\), \(a_2 = -1\)을 대입하면 영벡터가 생성됩니다. 0이 아닌 계수를 사용하여 영벡터를 생성했으므로 두 벡터 (1, 1)과 (2, 2)는 선형 의존이라고 볼 수 있습니다.
(1, 2)와 (2, 1)은 선형 의존인가? 선형 독립인가?
위 식은 다음과 같은 연립 방정식으로 정리할 수 있습니다.
$$ a_1(1,2)+a_2(2,1)=(a_1+2a_2,2a_1+a_2) $$
$$ a_1+2a_2=0 $$
$$ 2a_1+a_2=0 $$
위 식을 만족하는 값은 \(a_1 = 0\), \(a_2 = 0\) 뿐이므로, 따라서 두 벡터 (1, 2)와 (2, 1)은 선형 독립입니다.
그렇다면 이게 왜 필요한 걸까요? 바로 새로운 벡터를 생성해내는 시스템과 연관이 있기 때문입니다.
선형 조합으로 새로운 벡터 생성하기
예를 들어 벡터 (5, 5)를 두 벡터의 조합으로 생성한다고 가정해보겠습니다.

벡터 \(v_1 (1, 0) \)과 벡터 \(v_2 (0, 1)\)을 골랐다고 하면, 이걸 선형 조합하여 벡터 \((5, 5)\)를 만들 수 있을까요?
당연히 만들 수 있습니다. 각각에 5를 곱하면 되죠. 이것 외에도 다른 쌍이 존재할까요?
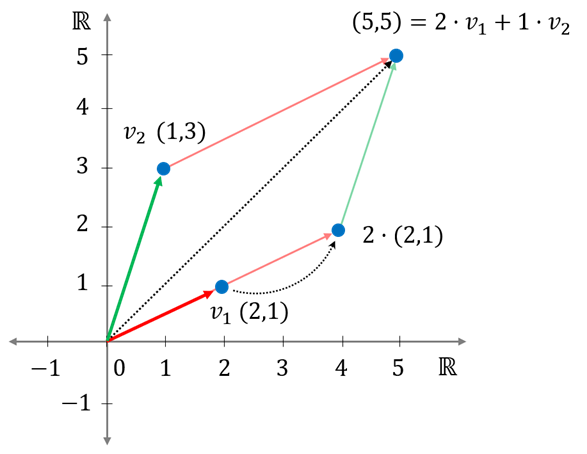
이번에는 \(v_1 (2, 1)\)과 \(v_2 (1, 3)\) 벡터를 골랐습니다. 이 벡터들을 선형 조합하여 \( (5, 5)\)를 만들 수 있을까요? 네. 역시 만들 수 있습니다.
$$ 1 \dot (1, 3) + 2 \dot (2, 1) = (5, 5) $$
두 벡터를 조합하여 평면 위의 모든 벡터 생성이 가능한가?
그렇다면 두 벡터 \((2, 1)\), \((1, 3)\)을 조합하여 평면 위의 모든 벡터 생성이 가능할까요? 이를 수식으로 나타내면 다음과 같습니다.
$$ (x,y)=a(2,1)+b(1,3) $$
위 수식은 다음의 연립 방정식처럼 쓸 수 있습니다.
$$ x=2a+b $$
$$ y=a+3b $$
위 식에서 \(a\)와 \(b\)를 구할 수 있기 때문에 모든 점의 생성이 가능하다는 결론을 낼 수 있게 됩니다.
따라서 \((2, 1)\)과 \((1, 3)\)을 조합해서 평면 위의 모든 벡터를 생성할 수 있습니다.
두 벡터를 조합하여 평면 위의 모든 점 생성이 가능한가?
그렇다면 모든 두 벡터의 조합은 평면의 모든 점을 생성할 수 있을까요?
벡터 \((1, 2)\)와 \((2, 4)\)가 있다고 하면,
$$ (x,y)=a(1,2)+b(2,4) $$
역시 이 경우도 연립 방정식으로 나타날 수 있습니다.
$$ x=a+2b $$
$$ y=2a+4b $$
위 연립 방정식의 해는 존재하지 않습니다. 오직 \((x, 2x)\) 형태의 벡터만 생성이 가능하죠. 다시 말해, \(y\)가 \(x\)의 두 배인 경우의 밖에 해가 존재하지 않다는 의미가 됩니다. 이 경우, 모든 벡터를 생성하는 것이 아니고 \(x\)와 \(y\)가 특별한 비율의 관계에 있을 때만 이 수식이 성립한다는 거죠.

이렇게 \(v_1 (1, 2)\)와 \(v_2 (2, 4)\)가 만들어 낼 수 있는 벡터는 \(y = 2x\)라는 직선 위에 존재하는 1차원적인 벡터만 생성해낼 수 있습니다. \((2, 4)\)는 사실상 \( 2(1, 2)\)의 스칼라 곱으로 표현되기 때문에 \(v_1 (1, 2)\)의 기울기와 동일한 벡터만 생성되기 때문이죠.
$$ (x,y)=a(1,2)+b(2,4) $$
$$ =a(1,2)+2b(1,2) $$
$$ =(a+2b)(1,2) $$
결론을 말씀드리자면 1)어떤 벡터들의 선형 조합은 평면 위의 모든 벡터들을 생성해낼 수 있고, 또 2)어떤 벡터들은 1차원 선에 있는 벡터들만 생성할 수 있다는 점입니다. 즉, 조합하려는 벡터들이 서로 선형 독립일 때만 평면 위의 모든 벡터들을 생성해낼 수 있다는 의미죠.
왜 이런지에 대해 설명은 다음에 하기로 하고, 우선 수학에서 설명하는 기저(basis)와 차원(Dimension)을 먼저 알아보죠.
2. 기저(Basis)와 차원(Dimension)
기저(Basis)
벡터 공간 내에 있는 모든 벡터들을 생성할 수 있는 선형 독립인 벡터들의 집합을 말합니다.
- 기저 벡터(Basis vector) : 기저 집합에 속한 원소
기저라는 것은 집합의 의미이고, 기저 집합의 원소는 당연히 벡터가 되므로 이걸 기저 벡터라고 부릅니다.
차원(Dimension)
기저 집합이 가지는 원소의 수를 말합니다. 여기서 말하는 차원은 인지 개념의 뜻으로 사용되는 차원이 아닙니다.
여기서 이야기하는 차원의 의미는 공간을 형성할 때, 사용되는 기저들이 가지고 있는 원소의 수를 말합니다.
2차원 평면을 생성하기 위해서는 항상 두 개의 기저 벡터가 필요한 것이죠. 위에서 예제를 볼 때, 벡터 \((5, 5)\)를 만들기 위한 벡터의 조합은 두 가지가 있었죠?
$$ B_1 : (1,0) , (0,1) $$
$$ B_2 : (2,1) , (1,3) $$
연립 방정식의 해가 존재한다면 모두 기저가 됩니다. 왜냐하면 모두 선형 독립이기 때문이죠. 연립 방정식의 해를 가지고 있는 벡터의 쌍은 항상 2개가 됩니다.
즉, \(B_1, B_2\) 모두 평면의 기저가 될 수 있고 무한히 많은 기저에 대한 경우의 수가 존재하지만, 기저 집합의 원소의 수는 언제나 두 개로 동일하다는 것이죠.
여기서 중요한 사실을 하나 알아야 하는데, 기저 원소가 2개 쓰이는 평면 환경에서 계속 생각해 봅시다.
만약 기저 원소가 하나라면 벡터와 스칼라의 곱셈 성질로 인해 하나의 선에 해당하는 벡터만을 생성할 수 있지만, 기저 원소가 평면 이상의 차원인 세 개 이상인 경우는 존재하지 않게 됩니다.
무슨 말이냐면, 앞선 식에서 두 선형 독립인 벡터로 평면 상의 모든 점을 생성할 수 있다는 것을 알았습니다.
그렇다면 아래 식의 경우, 영벡터를 만들기 위해 0이 아닌 세 번째 계수가 존재한다는 것을 의미하게 됩니다.
$$ (a_1v_1+a_2v_2)+a_3v_3= \vec{0} $$
$$ (-a_3v_3)+a_3v_3= \vec{0} $$
선형 조합인 \((a_1v_1+a_2v_2)\)으로 덧셈의 역원 \((-a_3v_3)\)을 생성해낼 수 있기 때문에 \(a_3\)는 0이 아니어도 영벡터를 생성할 수 있다는 결론을 내게 됩니다. 즉, 선형 독립이 아니게 되죠.
따라서 평면에서 세 개 이상의 원소로 구성된 기저는 존재하지 않는다는 걸 알 수 있었습니다.
실 벡터 공간을 표기할 때, 이러한 차원의 정보를 사용해 첨자를 붙여 다음과 같이 표기합니다.
$$ R^2, R^3 $$

표준 기저 벡터 (Standard basis vector)
- 기저 벡터 중에서 가장 기본이 되는 벡터
- 축에 따라 균등한 공간을 만들어내는데 기준이 됨
- \(\mathbb{R}^2\)의 표준 기저 벡터 \(e_1 :(1,0) \quad e_2 : (0,1)\)
- \(\mathbb{R}^3\)의 표준 기저 벡터 \(e_1 :(1,0,0) \quad e_2 : (0,1,0) \quad e_3 : (0,0,1) \)
'Computer Sciences > Game Mathemathics' 카테고리의 다른 글
| [게임 수학] #6 | 삼각함수(2) : 각의 측정법 (0) | 2022.07.25 |
|---|---|
| [게임 수학] #5 | 삼각함수(1) : 삼각함수의 개념 (0) | 2022.07.25 |
| [게임 수학] #3 | 벡터(Vector) (0) | 2022.07.20 |
| [게임 수학] #2 | 함수(Function) (0) | 2022.05.05 |
| [게임 수학] #1 | 수(Numbers)의 구조 (2) | 2022.05.05 |