[게임 수학] #5 | 삼각함수(1) : 삼각함수의 개념

인프런 <게임 엔진을 지탱하는 게임 수학, 이득수 교수님> 강의를 보며 공부한 글입니다.

 

 

 

1. 삼각함수(Trigonometric function)

수학에서 삼각함수는 각의 크기를 삼각비로 나타낸 함수를 의미합니다. 삼각비(Trigonometric ratios)란 직각삼각형의 세 변의 길이 중 두 변의 길이 간의 비례 관계를 나타내는 걸 말하구요. 이러한 삼각비에는 우리가 흔히 아는 사인(sin), 코사인(cos), 탄젠트(tan)가 있습니다.

 

이러한 삼각함수 개념에 대해 이해하려면, 우선 그 기반 개념인 직각삼각형과 삼각비에 대해 더 알아보도록 합시다.

 

직각삼각형(Right-Angled Triangle)

직각 삼각형의 요소들

 

 

직각삼각형은 다음과 같은 세 개의 요소로 이루어져 있습니다.

• 빗변 (Hypotenuse)  :  직각 맞은편의 비스듬한 변
• 밑변 (Adjacent)  :  직각 밑에 존재하는 변
• 높이 (Opposite)  :  빗변과 밑변을 제외한 나머지 변

 

이러한 직각삼각형의 형태에서부터 계산할 수 있는 것이 있습니다. 세 개의 변 중에 두 개의 변을 골라서, 그 두 개의 변에 대한 비율의 값을 구하는 것이죠. 이것을 삼각비(Trigonometric Ratio)라고 부릅니다. 

 

삼각비(Trigonometric Ratio)

직각삼각형을 구성하는 세 요소 중 두 요소에 대한 비의 값이라고 했죠?

총 6가지의 경우가 발생하지만, 흔히 자주 쓰이는 삼각비들이 3가지가 있습니다.

• $sin\theta =\frac{높이}{빗변}$
• $cos\theta =\frac{밑변}{빗변}$
• $tan\theta =\frac{높이}{밑변}$

 

이런 삼각비를 우리가 함수의 개념으로 확장할 수 있습니다.

 

삼각함수(Trigonometric Function)

직각삼각형이 가지고 있는 빗변과 밑변 사이에 있는 각($\theta$)을 정의역으로 두고, 이 비율의 값을 취하는 것이죠.

이 때, 이 값은 항상 -1 ~ 1 사이의 값을 가지게 됩니다. 아래와 같은 대응 관계가 생기는 것이죠.

• 정의역  :  실수 집합 $R$
• 공역  :  $[-1,1]$

 

 

 

이런 대응 관계를 삼각비에 대해 어떤 값을 대입했다는 의미로 위와 같이 함수로 표시할 수 있게 됩니다.

이것을 삼각함수라고 이야기하는 것이죠. 삼각비를 데카르트 평면 좌표계에서 만들어지는, 흔히 360도라 불리는 평면의 모든 각에 대해서 일반화시킨 대응 관계가 삼각함수라고 할 수 있겠습니다.

 

하지만 직각삼각형의 경우, 각($\theta$)이 0 ~ 90 사이로 한정될 수 밖에 없습니다. 그렇지 않으면 삼각형을 그릴 수 없기 때문이죠. (∵ 삼각형의 내각의 합은 180도)

 

그래서 이런 한계점을 극복하기 위해, 직각삼각형을 포함하는 원을 통해 삼각함수를 표현하는 방법을 사용하기로 합니다. 이 원을 단위원(Unit circle)이라고 부르죠.

 

---

2. 삼각함수와 단위원(Unit Circle)

단위원(Unit Circle)이라고 하는 것은 반지름 길이가 1인 원을 말합니다.

데카르트 좌표계에서 단위원과 삼각함수를 표현하면 다음과 같이 표현할 수 있습니다.

 

 

 

위와 같이 표현하게 되면, 단위원의 중심이 항상 원점에 존재하기 때문에 각($\theta$)만 변동한 경우에도 직각삼각형의 빗변의 길이는 항상 1이 됩니다. 이 상태에서 삼각함수를 지정하여 빗변 벡터를 한 바퀴, 두 바퀴 계속 돌리게 되면 다음과 같이 표현됩니다.

 

<출처> https://en.wikipedia.org/wiki/Sine#/media/File:Circle_cos_sin.gif

 

이것이 바로 사인(sin) 함수와 코사인(cos) 함수의 그래프입니다. 한 바퀴 돌고나면 리셋이 되지만, 사실 계속 돌고 있다고도 볼 수 있겠습니다. 반대 방향으로도 그렇구요. 이 말의 의미는 실수 집합에 있는 모든 값을 사용하고 있다고 볼 수가 있습니다.

 

 

 

사인(sin) 함수와 코사인(cos) 함수의 성질

1. 사인 함수와 코사인 함수는 항상 $[-1,1]$ 범위를 일정하게 반복되는 패턴을 가진다.
2. 사인 함수와 코사인 함수는 $2\pi (360도)$ 단위로 반복된다.
3. 축을 기준으로 좌우를 포갰을 때 코사인 함수는 좌우 대칭, 사인 함수는 상하가 반전된 형태를 띈다.

 

$$sin(\theta )\ne sin(-\theta )$$

$$sin(\theta )=-sin(-\theta )$$

$$cos(\theta )=cos(-\theta )$$

 

그런데 한 가지 신기한 사실이 있습니다. 탄젠트 함수는 cos 90°, cos 270°에서 값이 존재하지 않습니다. 왜 존재하지 않을까요?

 

 

 

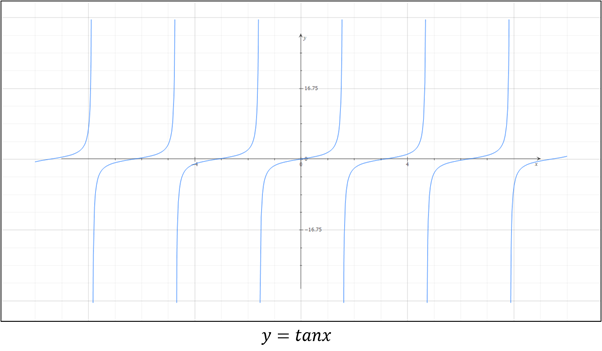
탄젠트 함수의 특정 값이 존재하지 않는 이유

다시 한 번, 단위 원의 직각 삼각형을 살펴보겠습니다.

 

 

 

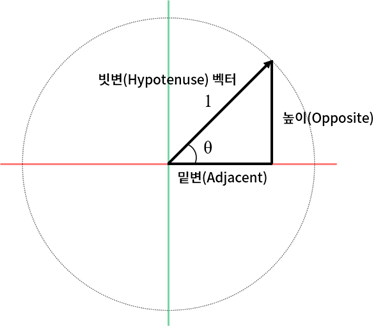
단위원에서 특정 각 $\theta$에 대한 좌표값으로, x값은 직각삼각형의 밑변 길이입니다. 그런데, 우리는 다음과 같은 사실을 알고 있죠.

 

$$cos\theta =\frac{밑변}{빗변}$$

 

빗변은 단위원의 반지름 길이이기 때문에 1이라서 다음과 같이 표현할 수 있습니다.

 

$$밑변=cos\theta$$

 

마찬가지로 높이에 대해서도 다음과 같이 표현할 수 있습니다.

 

$$높이=sin\theta$$

 

 

이 말은 다른 의미로는 단위원에서의 좌표값은 항상 $(cos\theta ,sin\theta )$라는 것을 의미하기도 하죠.

그렇다면 왜 탄젠트 함수는 cos 90°, cos 270°에서 값이 존재하지 않을까요? 탄젠트 삼각비는 다음과 같았습니다.

 

$$tan\theta =\frac{높이}{밑변}$$

 

그리고, 위에서 말했지만 단위원의 좌표값은 $(cos\theta ,sin\theta )$이 된다고 했습니다. 

즉, 분모인 밑변에 $cos\theta$ 값이 들어가게 되죠. 하지만 $cos\theta$ 값은 90도와 270도에서 0이라는 값을 가지게 됩니다. 분모에는 0이 들어갈 수 없기 때문에 90도와 270도에서 탄젠트 함수의 값이 존재하지 않는 것입니다. 

 

 

삼각함수의 유용한 공식

직각삼각형이기 때문에 피타고라스의 정리를 삼각함수에도 적용할 수 있습니다.

 

$$밑{변}^2+높{이}^2=빗{변}^2$$

 

이것을 단위원 직각삼각형에 그대로 적용하게 되면 다음과 같은 식을 도출해낼 수 있습니다.

 

$$(cos\theta {)}^2+(sin\theta {)}^2=1^2$$

 

 

단위원이 아닌, 원의 반지름 값이 $r$이라고 특정되는 경우에도 역시 유효하게 사용할 수 있습니다. 이 때는 원호의 좌표는 $(cos\theta ,sin\theta )$ 벡터에 $r$배 곱한 결과가 나오게 되죠. (벡터와 스칼라의 곱셈이 생각나지 않나요?)

 

 

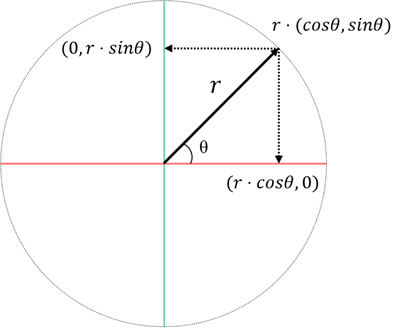
이 역시 삼각비를 이루기 때문에 공식 또한 유효하게 됩니다.

 

$$r^{2}co{s}^{\theta }+r^{2}si{n}^{\theta }=r^2$$

$$\therefore co{s}^2\theta +si{n}^2\theta =1$$

 

 

또한 원호의 위치한 좌표를 x값과 y값으로 분해할 수도 있습니다.

벡터와 벡터의 덧셈, 벡터와 스칼라의 곱셈을 이용하면 말이죠.

 

$$r\cdot (cos\theta ,sin\theta )=(r\cdot cos\theta ,0)+(0,r\cdot sin\theta )$$

 

 

또한 알아두면 좋은 지식으로 실 벡터공간 ${\mathbb{R}}^2$의 표준 기저 벡터에 $(1,0),(0,1)$이 있었죠?

이것들도 결국에는 크기가 1인 벡터인 셈입니다. 이것은 일반화를 시킬 수 있다고 했을 때, 평면에 크기가 1인 모든 벡터들은 $(cos\theta ,sin\theta )$으로 일반화 할 수 있습니다.

 

이렇게 일반화 한 벡터들 중, 두 종류가 $(1,0),(0,1)$라는 것이죠. 이 두 벡터는 각각 각도가 0도, 90도에 해당하는 벡터를 의미한다고 볼 수 있습니다.

 

$$e_1=(cos(0),sin(0))=(1,0)$$

$$e_2=(cos(90),sin(90))=(0,1)$$