[게임 수학] #8 | 행렬(Matrix)

인프런 <게임 엔진을 지탱하는 게임수학, 이득우 교수님> 강의를 듣고 공부한 글입니다.

 

 

 

1. 행렬(Matrix)

 

벡터가 하나의 행 또는 열만을 표현할 수 있는 것에 비해, 행렬은 행 벡터(Row vector) 혹은 열 벡터(Column vector)들을 활용하여 2차원으로 구성이 가능합니다. 이러한 행렬은 컴퓨터 그래픽스에서 점이나 오브젝트 등을 다른 위치로 옮기거나 회전하는 등의 변환 연산에 주로 사용됩니다.

 

행렬이란 것은 단순하게 정의하면, 어떤 사각형 틀 안에 행과 열을 맞춰서 수를 나열한 것에 불과합니다.

다시 말해, 가로를 행(Row), 세로를 열(Column)이라고 하는 특정한 사각형 틀에 스칼라 값들을 나열하는 것이죠.

예를 들어, \( 2 \times 3 \) 의 A라는 이름의 행렬을 다음과 같이 표기할 수 있습니다.

 

$$ A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix} $$

 

이렇게 표현하는 행렬 자체에 무언가 특별한 의미가 있다기 보다는, 편리하게 계산할 수 있도록 배치한 것이라고 보면 되겠습니다.

 

 

행렬의 연산

 

행렬과 행렬의 덧셈

 

크기가 같은(행과 열의 개수가 같은) 행렬에만 적용이 가능하며, 각 원소 위치에 해당하는 값들을 서로 더하고 동일한 위치에 지정해주면 됩니다.

 

\begin{align} A+B &= \begin{bmatrix} a & b  \\ c & d \end{bmatrix} + \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} a+e & b +f \\ c + g & d +h \end{bmatrix}\end{align}

 

행렬과 스칼라의 곱셈

 

모든 행렬 원소에다가 스칼라 값을 곱해주는 연산을 수행해주면 됩니다.

 

\begin{align} k \cdot A &= k \cdot \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} ka & kb \\ kc & kd \end{bmatrix} \end{align}

 

행렬의 전치(Transpose) 연산

 

전치(Transpose)는 행과 열을 바꿔치기 하는 연산을 의미합니다. 즉, 행이 열이 되고, 열이 행이 되는 것이죠.

 

\begin{align} \begin{bmatrix} a & d \\ b & e \\ c & f \end{bmatrix}^T = \begin{bmatrix} a & b & c \\ d & e & f \end{bmatrix} \end{align}

 

행렬과 행렬의 곱셈

 

두 행렬의 곱셈 \(A \times B \)를 수행하려면, "앞에 있는 행렬(\(A\))의 열 개수 = 뒤에 있는 행렬(\(B\))의 행 개수" 여야 합니다. \(A(m \times n) \cdot B(n \times p) \) 이런 경우에만 곱셈이 가능하다는 말이죠. 이렇게 곱셈을 해서 나오는 행렬 \(C\) 는 \(A\) 행렬의 행 개수인 \(m\)과 \(B\) 행렬의 열 개수인 \(p\)만큼의 사이즈인 \(m \times p \)의 크기가 됩니다.

 

$$ C(m \times p) = A(m \times n) \cdot B(n \times p) $$

 

 

곱셈을 하는 방법은 조금 복잡합니다. 앞 행렬은 행 벡터(가로 방향) 순서대로, 뒷 행렬은 열 벡터(세로 방향) 순서대로 각 원소를 곱해 더하면 됩니다.

 

\begin{align} A \cdot B = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \\ ce + dg & cf + dh \end{bmatrix} \end{align}

 

 

이러한 곱셈 연산과 관련하여 중요하게 알아야 할 사실이 있습니다.

 

교환 법칙을 만족하지 않는다.

 

\begin{align} A \cdot B = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \\ ce + dg & cf + dh \end{bmatrix} \end{align}

 

\begin{align} B \cdot A = \begin{bmatrix} e & f \\ g & h \end{bmatrix} \cdot \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} ae + cf & be + df \\ ag + ch & bg + dh \end{bmatrix} \end{align}

 

$$ A \cdot B \ne B \cdot A $$

 

결합 법칙은 성립한다.

 

$$ A \cdot (B \cdot C) = (A \cdot B) \cdot C $$

 

즉, 무엇을 먼저 곱하든 간에 기존의 순서만 유지된다면 동일한 결과를 보장한다는 것이죠.

이러한 행렬의 성질은 아주 큰 이점을 가지게 됩니다. 그 내용은 뒤에서 보도록 하죠.

 

 

전치 연산

 

$$ (A \cdot B)^T = B^T \cdot A^T $$

 

\begin{align} (A \cdot B)^T = \begin{bmatrix} ae+bg & af +bh \\ ce + dg & cf + dh \end{bmatrix}^T = \begin{bmatrix} ae + bg & ce +dg \\ af +bh & cf +dh \end{bmatrix} \end{align}

이것은 다음과 같습니다.

\begin{align} B^T \cdot A^T = \begin{bmatrix} e & g \\ f & h \end{bmatrix} \cdot \begin{bmatrix} a & c \\ b & d \end{bmatrix} = \begin{bmatrix} ae + bg & ce + dg \\ af + bg & cf +dh \end{bmatrix} \end{align}

 

 

분배 법칙

 

행렬의 덧셈과 곱셈을 사용한 분배 법칙도 만족합니다.

 

$$ A(B+C) = AB + AC $$

$$ (B+C)A = BA + CA $$

 

다만, 위에서 보이는 것처럼 행렬 \(A\)가 좌측에서 분배된다면, 각 행렬의 곱셈 결과에는 \(A\)가 좌측에 있어야 합니다. 반대로, 행렬 \(A\)가 우측에서 분배된다면, 각 행렬의 곱셈 결과에 \(A\)가 우측에 있어야 합니다.

이것 역시 교환 법칙이 성립하지 않는 행렬의 특성에서 나온 주의점인 것 같네요.

 

 

 

---

2. 선형 변환과 행렬

 

벡터 공간의 구조를 그대로 유지하면서 선형성을 띄는 선형 변환을 통해, 새로운 공간으로 변환되는 그 과정 자체가 행렬에 대응된다는 점이 있고, 이것이 행렬을 사용하는 이유입니다. 1)복잡한 선형 변환식을 일일이 계산하지 않아도 되며, 2)행렬로 정리된 간편한 식의 곱셈 전개를 통해 원하는 선형 변환을 빠르게 구현할 수 있다는 장점이 있습니다.

 

앞 전에 선형성 파트에서, \( \mathbb{R}^2 \mapsto \mathbb{R}^2 \) 대응관계를 가지는 다음 벡터 함수는 선형성을 만족한다는 것을 알아봤습니다.

 

$$ f((x,y))=(ax+by, cx+dy) $$

 

위와 같은 선형 변환식은 어떻게 행렬식으로 바꿀 수 있을까요? 어떤 임의의 행렬 \(A \)를

 

\begin{bmatrix} a & b \\ c & d \end{bmatrix}

 

라고 정의하고, 임의의 벡터 \(v\)를

 

\begin{bmatrix} x \\ y \end{bmatrix}

 

를 정의했을 때, 행렬과 행렬의 곰셉 법칙에 의해서 다음과 같은 결과가 나옵니다.

 

\begin{align} A \cdot v = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix} \end{align}

 

 

위 식을 보면, 선형 변환식에서 원래 사용되었던 \(x, y\) 가 열 벡터 \(v\) 로 존재하고, \(ax+by\) 를 첫 번째 요소로, \(cd+dy\) 를 두 번째 요소로 가지는 결과물이 만들어지게 됩니다.

 

그렇다면, 위 식에서 곱했던 행렬 \(A\)는 무엇일까요?

바로, \((ax + by, \ cx+dy) \) 이라고 하는 어떤 점으로 대응시켜주는 선형 변환 함수의 역할을 하는 것입니다.

 

 

이러한 결과들을 통해, 우리는 다음과 같은 의미를 추론할 수 있습니다.

• \(A\) 행렬은 같은 차원의 공간이 서로 대응되도록 하는 선형 변환
  • 즉, 정방 행렬은 같은 차원의 공간이 서로 대응되도록 하는 선형 변환임을 의미
  • \(A\) 행렬은 \(2 \times 2 \) 정방 행렬이었으므로, \( \mathbb{R}^2 \mapsto \mathbb{R}^2 \) 
• 열 벡터는 벡터 공간의 벡터

 

 

열 기반 행렬과 행 기반 행렬

 

벡터를 행으로 표현하냐, 열로 표현하냐에 따라 방법이 두 가지가 있습니다.

열 기반 행렬(Column Major Matrix)는 수학에서 사용하는 기본 방식이며, OpenGL에서 사용하고 있습니다.

벡터의 순서가 뒤에 온다는 특징이 있으며, 결과 또한 열의 결과로 나오는 걸 볼 수 있습니다.

 

\begin{align} \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix} \end{align}

 

 

행 기반 행렬(Row Major Matrix)는 DirectX 및 게임 엔진에서 사용하는 방식입니다. 벡터의 순서가 앞에 온다는 특징이 있으며, 결과 또한 행의 결과로 나오는 걸 볼 수 있습니다.

 

\begin{align} \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} a & c \\ b & d \end{bmatrix} = \begin{bmatrix} ax + by & cx + dy \end{bmatrix} \end{align}

 

 

허나, 사실상 열 기반 행렬과 행 기반 행렬은 서로 전치 관계일 뿐, 결과는 동일함을 보장합니다.

 

$$ Av = v' $$

$$(v')^T = (Av)^T = v^TA^T $$

 

 

---

3. 선형 변환의 시각화

 

변환되기 전의 어떠한 벡터 공간 \((x, y) \) 가 있다고 가정해 봅시다. 여기에서 \( x, \ y \) 는 서로 균일하게 동등한 관계에서 똑같이 간섭 없이 조합됐다고 볼 수 있습니다. 즉, 선형 독립인 거죠.

 

그렇기에, 이러한 임의의 점 \((x, y)\) 를 어떻게 생성했는지 구조를 생각해 본다면, 표준 기저 벡터 \(e_1(1, 0)\) 과 \(e_2(0, 1)\) 에다가 각각 \(x\) 배, \(y\) 배 해서 더했다고 볼 수 있습니다. 선형 변환을 하기 전, 원래 벡터 공간에 속한 임의의 벡터에 대한 조합식이 다음과 같다고 생각해 봅시다.

 

$$ (x, y) = x(1, 0) + y(0, 1) $$

 

그리고 선형 변환 함수 역할을 하는 다음과 같은 A 행렬이 있다고 합시다.

 

\begin{align} A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \end{align}

 

이 때, A 행렬을 각 열 벡터로 나누어 보게 된다면 \( (a, c) \), \( (b, d) \) 가 되고, 이것은 변화된 공간의 표준 기저 벡터 \( e_1'(a, c), e_2'(b, d) \) 를 의미합니다. 이 말은 기존의 벡터 공간을 이루고 있던 표준 기저 벡터 \(e_1(1, 0), \ e_2(0, 1) \) 가 A 행렬의 각 열 벡터 성분으로 변화되었다라고 해석할 수 있겠지요.

 

$$ x(1, 0) + y(0, 1) \rightarrow x(a, c) + y(b, d) $$

 

([왼쪽] 변환 전 공간, [오른쪽] 변환 후 공간

 

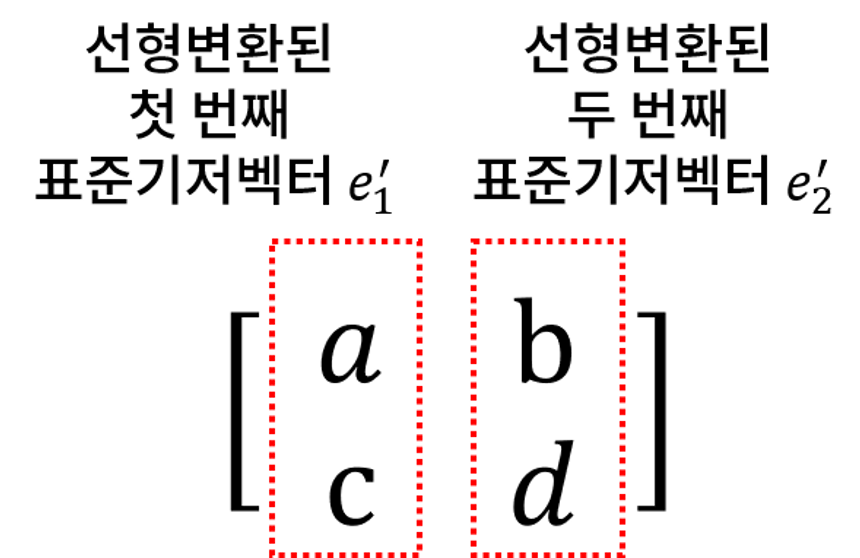
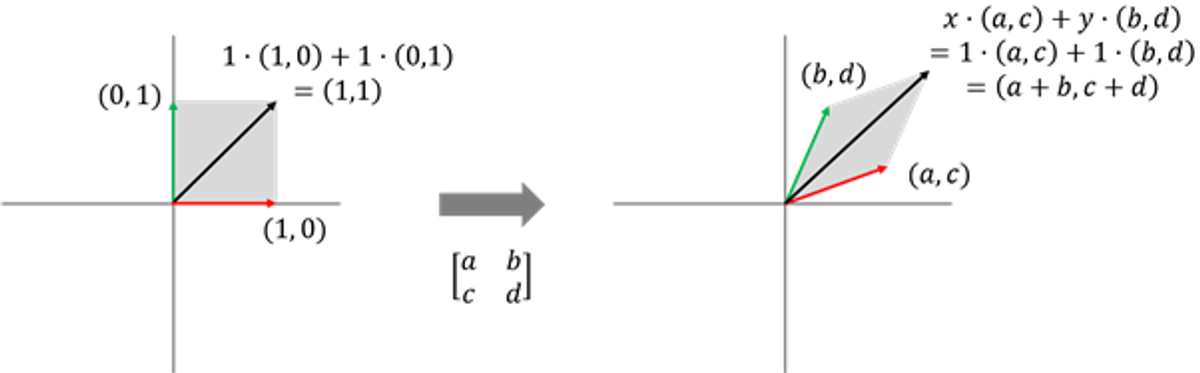
이렇게 선형 변환된 기저 벡터를 조합해, 변화된 공간의 모든 벡터들을 일일이 추적하지 않아도 알아낼 수 있게 됩니다.

 

$$ (x',y')=x(a,c)+y(b,d)=(ax+by, cx+dy) $$

 

그런데, 이 식 어디서 많이 보지 않았나요?

 

$$ f((x,y))=(ax+by, cx+dy) $$

 

네. 앞서 살펴 봤었던 선형 변환식과 똑같다는 걸 알 수 있습니다.

이런 식으로 표준 기저 벡터를 변환할 수 있다면, 원하는 변환을 쉽게 적용할 수 있게 됩니다.

 

예) 크기 변환 행렬

 

다음과 같은 원래 평면 공간에 존재하는 물체를 좌우로는 A 만큼 늘리고, 상하로는 B 만큼 줄이려고 합니다.

그러면, 기존 평면을 이루던 공간의 표준 기저 벡터 \( e_1(1, 0), \ e_2(0, 1)\) 에 변환시켜 줄 행렬을 적용해야 겠지요.

가로로는 A 만큼 늘리고, 세로로는 B 만큼 줄인다고 했으니까 다음과 같은 행렬을 사용하면 될 겁니다.

 

\begin{align} \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ax + by \end{bmatrix} \end{align}

 

[왼쪽] 원래 평면 표준 공간 [오른쪽] 크기 변환을 적용한 결과

 

 

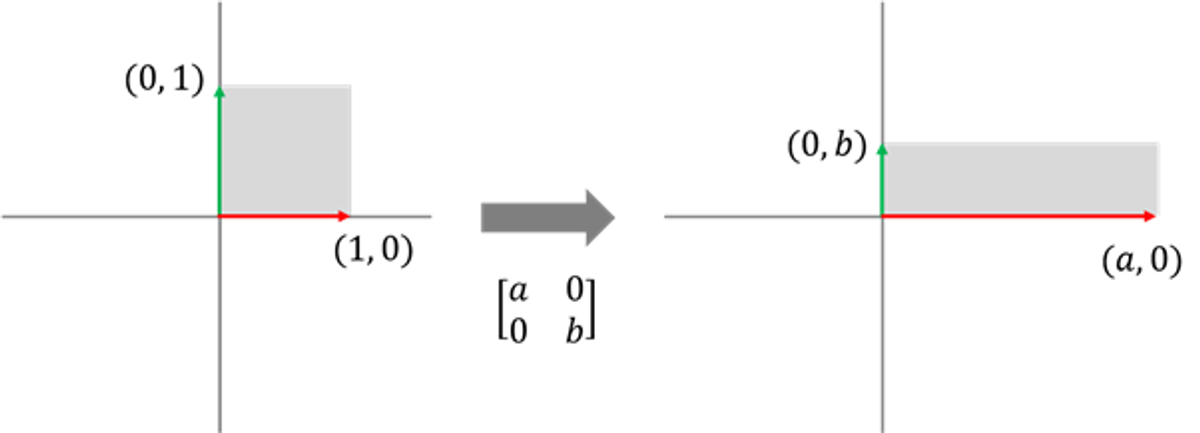
예) 밀기 변환

 

이번에는 y축만 x축 방향으로 \(a\) 칸 미는 변환을 해봅시다. x축은 변화가 없으니 (1, 0) 그대로 사용해주면 될 것이고, 대신 y축이 기존 위치에서 \(a\)만큼 오른쪽으로 밀어지는 거니 \((a, 1)\)을 사용하면 됩니다.

 

\begin{align} \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x + ay & y \end{bmatrix} \end{align}

 

[왼쪽] 원래 평면 표준 공간 [오른쪽] 밀기 변환을 적용한 결과

 

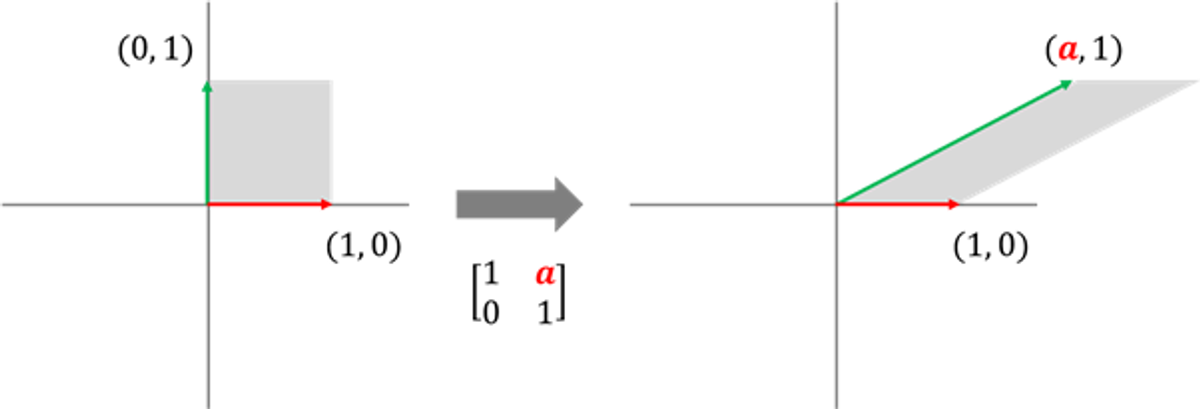
예) 임의의 각 \(\theta \)에 대한 회전

 

표준 평면 공간에서 임의의 각 \(\theta \) 만큼 회전을 하게 되면, 표준 기저 벡터 \(e_1, \ e_2 \) 는 각각 다음과 같이 좌표가 변화하게 됩니다.

 

[왼쪽] 원래 평면 표준 공간 [오른쪽] 회전한 결과

 

\(e_1\) 이 \( (cos \theta, \ sin \theta)\) 로 변화해야 하고, \(e_2\) 가 \( (-sin \theta, \ cos \theta) \) 로 변화해야 하니, 다음과 같이 적용해주면 됩니다.

 

$$ \begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} =\begin{bmatrix} xcos\theta-ysin\theta & xsin\theta+ycos\theta \end{bmatrix} $$

 

 

---

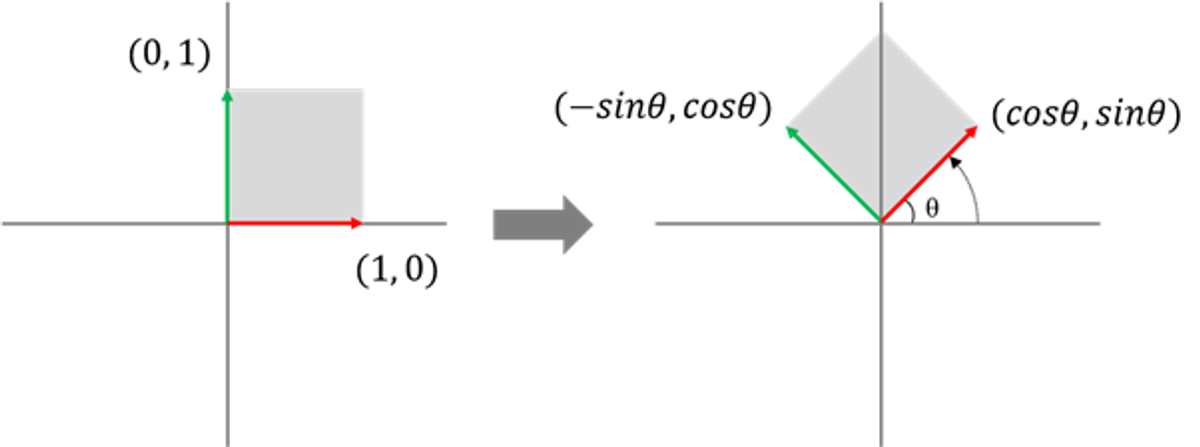
4. 행렬의 곱이 가지는 특징

 

행렬은 하나의 선형 변환에 대응되며, 행렬의 곱은 선형 변환을 적용한 결과에 다시 선형 변환을 적용하는 과정을 거쳐 공간을 변환시키게 됩니다.

 

 

 

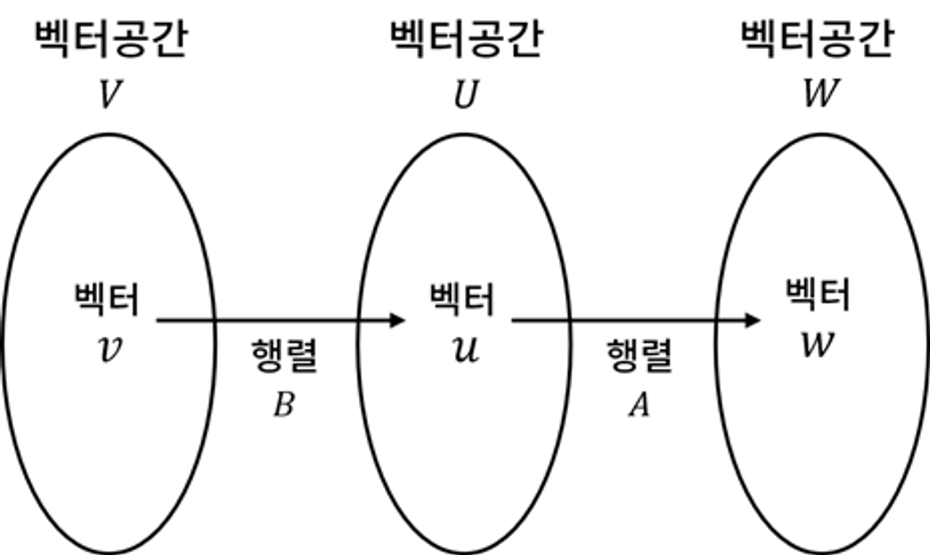
이를 수식으로 나타내면 다음과 같습니다.

 

$$ W = A\cdot (B\cdot v) $$

 

그런데, 행렬은 결합 법칙이 성립하므로 위 식은 다음과 같이 쓸 수 있습니다.

 

$$ W = (A\cdot B)\cdot v $$

 

즉, 기존 벡터 공간 \(v\)에 변환 행렬 \(A \)와 \(B\)를 곱한 결괏값을 \(v\)와 곱하게 되면, 바로 변환된 벡터 공간 \(W\)를 얻을 수 있다는 의미가 되죠. 즉, 합성함수처럼 한 방에 중간 단계를 거치지 않고, 한 방에 건너뛰기가 된다는 소리입니다.

 

이러한 의미를 가지기에, 두 행렬을 곱한 식 \(A \cdot B \)는 벡터 공간 \(V\)에서 벡터 공간 \(W\)로 직행할 수 있게 해주는 변환 함수의 의미를 가지게 된다고 볼 수 있습니다.

 

 

 

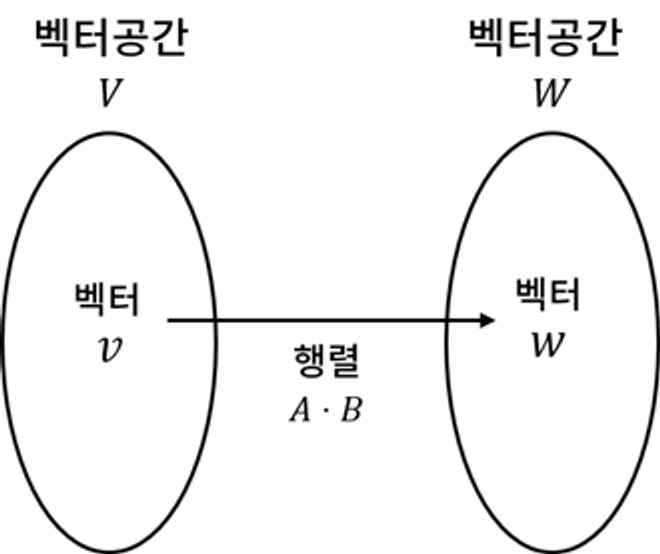
이러한 특징은 계산 과정을 많이 줄여주는 효과를 가져올 수 있기 때문에, 게임에서 행렬이 필수적으로 쓰이는 것입니다.

예를 들어, 게임 개발을 하다 보면 다음과 같은 5가지 변환을 주로 하게 됩니다.

• 크기 (S, Scale)
• 회전 (R, Rotation)
• 이동 (T, Translation)
• 뷰 (V, View)
• 투영 (P, Projection)

 

만약 어떠한 캐릭터가 10만 개의 점으로 이루어져 있다고 한다면, 이를 연산하여 모니터에 보여주기까지 위의 5가지 과정을 거치기에 50만번의 연산이 발생하게 됩니다.

 

$$ P\cdot (V\cdot (T\cdot (R\cdot (S\cdot v)))) $$

 

그런데, 위와 같은 5가지 변환들이 항상 고정되어 있다면, \(PVTRS\)를 미리 계산해 행렬로 생성한 후, 이를 사용하면 동일한 결과를 만들어주는 연산이 되므로 10만번으로 해결할 수 있게 됩니다.

 

$$ P\cdot (V\cdot (T\cdot (R\cdot (S\cdot v))))=(PVTRS)\cdot v $$

 

 

지금까지 행렬에 대해 알아보는 시간을 가졌습니다.