[게임 수학] #1 | 수(Numbers)의 구조

인프런 <게임 엔진을 지탱하는 게임 수학, 이득우 교수님> 강의를 듣고 필기한 글입니다.

 

 

1. 수의 시각화

수(Number)에 대해서 알아야 하는 이유

• 게임 세계는 벡터(Vector)로 구성된 탄탄한 시스템을 기반으로 함. 해당 시스템 위에서 컨텐츠가 만들어짐
• 이런 벡터는 수들을 조합하여 만들어진 대상
• 벡터를 정확히 이해하기 위해서는 결국 수가 만들어내는 시스템에 대해 이해해야 함

 

수의 종류

• 수는 물건을 세는 것에서 출발해 인류 문명의 발전에 맞춰 다양한 개념으로 확대되어 옴
• 다양한 수의 개념들이 존재하며, 각각은 대문자를 사용해 집합으로 구분해 부름
  • 자연수, 정수, 유리수, 무리수, 실수, 복소수 등

 

<출처>&nbsp;https://commons.wikimedia.org/wiki/File:Venn_Diagram_of_Numbers_Expanded.svg

 

 

실수 집합(The set of real numbers)

• 원소인 수와 수 사이에 빈틈 없이 연속된 원소들로 채워져 있는 수 집합
• 개념적으로 수와 수 사이에 빈틈이 없어야 하므로, 무한대의 수 원소들이 나열되어 있다.
• 실수 집합에 대한 개념과 실수 원소에 대한 개념을 혼동하지 않도록 주의

 

실수 집합

 

수직선(Number Line)

• 그렇다면, 집합을 표현할 때 원소들을 어떻게 나열하냐에 따라서 집합의 형태가 결정될 것임
• 하나의 원소를 점(Point)으로 표현한다면, 각 원소들을 빈틈 없이 연속적으로 표현한다면 쭉 이어진 형태로 표현됨
• 그렇기 때문에 실수 집합은 직선의 형태로 시각화가 가능함
• 이것을 수직선(Number Line)이라고 함

 

수 직선

 

수의 표현

• 수직선 위에 어떤 원소를 표기한다고 하면, 작은 수는 왼쪽, 큰 수는 오른쪽에 두고 대소를 비교하는 방식을 많이 사용함
• 하지만 벡터 시스템에 익숙해지기 위해선, 수를 바라보는 방법을 다르게 하는 것이 유리

 

하나의 체계에서 대소를 비교해 나열하는 방식

 

• 수직선이라는 하나의 체계에 기반해서 보는 것이 아니라, 0을 기준으로 왼쪽과 오른쪽으로 나누어진 대칭된 두 개의 체계로 보는 것이 더 편리
• 이러한 관점에서 본다면, 0을 기준으로 하여 어떤 수가 가지고 있는 요소는 두 가지로 요약될 수 있음
  
  1.  원점으로부터의 거리    ⇒   크기
  2.  원소 자신이 속한 세계  ⇒   방향

양수와 음수 두 체계로 나누고 크기와 방향을 사용해 표현하는 방식

 

 

---

2. 이항 연산(Binary Operation)

• 수에 대해서 표현을 할 수 있게 됐다면, 그 다음으로 알아야 할 것은 수가 가지고 있는 연산 시스템
• 위에서 수를 집합의 개념으로 관리한다고 얘기했지만, 집합이란 것은 사실 원소들의 묶음이라는 단순한 개념
  • 예를 들어, 우리가 사용하는 물건들을 모아서 묶음으로 만들면 그것 또한 집합
• 하지만 수 집합은 일반적인 집합과 달리, 그들 내의 연산이라는 시스템이 존재
• 이러한 수 집합의 연산을 보통 이항 연산(Binary Operation)이라고 함

 

 

• 위 그림에서 볼 수 있듯, 수 집합에 속한 어떤 원소 둘을 그들만의 정의된 연산을 통해 새로운 결과물을 생성해내는 작업이라고 볼 수 있음
  • \(a\)와 \(b\) 원소 둘을 º  연산을 통해 만들어낸 새로운 결과물, \(a \circ b\) 가 다시 집합에 속하게 됨
  • 이런 것을 수학에서는 닫혀 있다라고 표현함

 

사칙 연산의 재구성

• 흔히 알고 있는 사칙 연산 또한 바라보는 관점을 재조정할 필요가 있음
• 뺄셈과 나눗셈을 별도의 연산이 아닌, 덧셈과 곱셈 연산의 일부라고 생각
• 그렇다면 다음과 같이 뺄셈은 덧셈으로, 나눗셈은 곱셈으로 대체하여 표현이 가능

 

$$ 5 - 3 = 5 + (-3) $$

$$ 5 \div 3 = 5 \times \frac{1}{3} $$

 

 

덧셈 연산(Addition)의 시각화

• 덧셈 연산은 점을 평행 이동시키는 연산

 

 

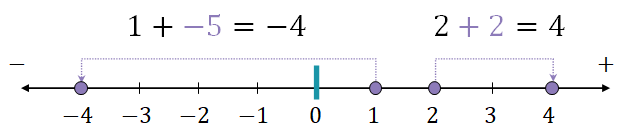
곱셈 연산(Multiplication)의 시각화

• 곱셈 연산은 원점을 중심으로 점의 크기와 방향을 조절하는 연산
• 그래서 사실 곱셈이라는 연산은 회전이란 개념이 포함되어 있다고 생각하면 됨
  • 양수의 곱셈은 0˚ 회전 (즉, 회전의 방향은 그대로 유지)
  • 음수의 곱셈은 180˚ 회전

 

 

 

---

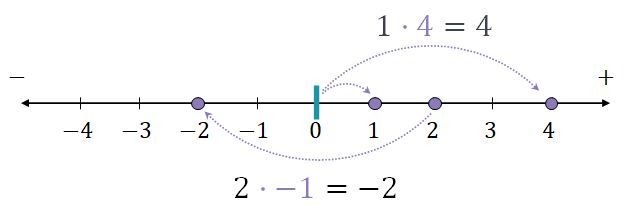
3. 이항 연산의 성질

• 실수 집합은 구조적인 측면에서 실수라는 무한한 원소를 가진 집합에 연산 체계가 들어가 있는 것이라고 설명했음
• 이런 이항 연산에 대해 가지고 있는 성질은 다음과 같이 있다.
  1. 교환 법칙(Commutativity)  :  \(a \cdot b=b \cdot a\)
  2. 결합 법칙(Associativity)  :  \((a\cdot b)\cdot c=a\cdot (b\cdot c)\)
  3. 분배 법칙(Distributivity) :  \(a\cdot(b+c)=a\cdot b+a\cdot c \quad (b+c)\cdot a =b\cdot a+c\cdot a\)

 

항등원(Identity)

• 어떤 임의의 요소에 대해 이항 연산의 결과가 동일한 원소로 나왔다고 할 때, 이런 결과를 만들게끔 해주는 또 다른 원소를 항등원이라고 한다. 

 

원소 a가 결과에서 또한 a 그대로 나오게 해주는 항등원은 b

 

• 덧셈의 항등원  :  \(a + 0 = a\)        ⇒  어떤 수를 더해서 원래 값 그대로 나오는 것은 0 밖에 없음
• 곱셈의 항등원  :  \(a \cdot 1 = a\)  ⇒  어떤 수를 곱해서 원래 값 그대로 나오는 것은 1 밖에 없음

 

역원(Inverse)

• 이항 연산의 결과가 항등원이 되도록 만들어 주는 특수한 원소를 의미
• 연산에 대한 항등원을 \(b\)라고 할 때, \(\circ\) 연산에 대한 \(a\)의 역원은 \(c\)

 

 

• 덧셈의 역원  :  \(a + -a = 0\)
  • 덧셈의 역원은 어떤 수에 대해 반대의 부호를 갖도록 만들어 줘야 함
  • 위처럼, 어떤 수에 대해 반대의 부호를 붙인 것을 반수(Opposite Number)라고 함 
• 곱셈의 역원  :  \(a\cdot \frac{1}{a} = 1, a\ne 0\)
  • 곱셈의 역원은 어떤 수에 대해 분모를 취하여 분수로 만들어 줘야 함
  • 이런 수를 역수(Reciprocal)라고 함

 

위에서 배운 내용들로 종합해봤을 때, 다음으로 정리할 수 있음

 

1. 뺄셈은 덧셈의 역원을 더하는 연산  :  \(a - b =a + (-b)\)
2. 나눗셈은 곱셈의 역원을 곱하는 연산  :  \(a\div b = a\cdot \frac{1}{b}\)

 

이렇게 뺄셈과 나눗셈 연산들을 사용하지 않고, 덧셈과 곱셈 연산으로 표현하는 이유는 뺄셈과 나눗셈 연산들은 교환 법칙이 성립하지 않기 때문

 

$$ a-b\ne b-a $$

$$a+(-b)=(-b)+a $$

 

 

---

4. 체(Field)의 공리(Axiom)

• 이제 덧셈과 곱셈이라는 두 가지 연산만을 사용하여, 실수가 가지고 있는 어떤 연산의 구조를 분석해볼 것임
• 어떤 수가 가지고 있는 체계를 분석할 때, 공리(Axiom)라는 것을 이용하여 분석을 하게 됨
• 공리(Axiom)란, 이론 체계에서 증명이 필요없는 가장 기초적인 명제
• 공리를 사용하여 다양한 수의 구조를 정의할 수 있음

 

첫 번째 연산에 대한 공리들

군(Group)의 공리

• 첫 번째 연산에 대해 다음의 공리를 만족하는 수의 체계를 말함
  
  1. 덧셈 연산에 대해 닫혀 있다. (Closure)   ⇒   덧셈의 결과는 항상 그의 수 집합에 속해야 함
  2. 덧셈 연산은 결합 법칙을 만족한다. (Associativity)
  3. 덧셈 연산의 항등원이 존재한다. (Identity element)
  4. 덧셈 연산의 역원이 존재한다. (Inverse element)

 

위의 공리들로 보았을 때, 실수는 군의 구조를 가진다고 이야기할 수 있다.

이 문장을 다음과 같이 표기할 수 있다.

 

$$  (\mathbb{R},+) $$

 

 

아벨 군(Abelian Group)

• 군의 공리에서 추가적인 조건으로, 교환 법칙이 만족한다. (Commutativity)

 

두 번째 연산에 대한 공리들

환(Ring)의 공리

• 첫 번째와 두 번째 연산에 대해 다음의 공리를 만족하는 수의 체계를 말함
  1. 곱셈 연산에 대해 닫혀 있다. (Closure)
  2. 곱셈 연산은 결합 법칙을 만족한다. (Associativity)
  3. 덧셈과 곱셈 연산은 분배 법칙을 만족한다. (Distributivity)

 

 

이런 환의 구조를 만족하는 것을 기호로 표기하면 다음과 같다.

 

$$ (\mathbb{R},+, \cdot) $$

 

 

가환환(Commutative Ring)

• 환의 공리에서 조금 더 빠듯한 조건을 추가한 공리
  1. 곱셈 연산은 교환 법칙을 만족한다. (Commutativity)
  2. 곱셈 연산의 항등원이 존재한다. (Identity element)
• 환의 구조에서 두 번째 연산에 대해 교환 법칙을 만족하고, 곱셈 연산의 항등원이 존재하는 특수한 환을 말함

 

체(Field)의 공리

• 곱셈의 역원이 존재하는 수의 구조
  1. 0을 제외한 모든 원소에 대해, 곱셈 연산의 역원이 존재한다. (Inverse element)
• 덧셈과 곱셈 연산에 대해 교환, 결합, 분배 법칙을 만족하고 항등원과 역원이 존재하는 수의 구조
• 사칙 연산에 닫혀 있고, 자유롭게 연산 순서를 적용할 수 있는 수의 구조
• 체의 구조를 만족하는 수 집합으로는 유리수, 실수, 복소수가 있음

 

 

실질적으로 수를 다룰 때 대부분 실수를 사용하지만, 이론적인 체계에서는 체의 구조를 가진 수 집합을 사용한다고 표현하는 것이 명확하고 확장 가능성이 높아진다. 체 집합은 \(F\)로 표현하고, 체 집합의 원소를 스칼라(Scalar)라고 한다.

 

 

 

 

---

Final. 다시 살펴보기

 

$$ a + b $$

 

• 위와 같은 연산을 바라볼 때, 이제는 두 가지 관점에서 바라볼 수 있게 되었음
  1. 실수 \(a\) 와 실수 \(b\) 를 더한다  :  사칙 연산을 자유롭게 사용할 수 있으나, 하나의 수 체계만 사용하기 때문에 결과물이 항상 실수로만 떨어지는 한계 존재
  2. 스칼라 \(a\) 와 스칼라 \(b\) 를 더한다  :  체의 성질을 만족하는 모든 수 집합(유리수, 실수, 복소수)에 대해 포괄적으로 사용 가능
     • 범용적인 수와 연산 시스템을 규정하는 체의 기반 위에서 새로운 시스템으로 확장하여 해석이 가능해짐