2023. 11. 24. 17:35ㆍComputer Sciences/Game Mathemathics
인프런 <게임 엔진을 지탱하는 게임수학, 이득우 교수님> 강의를 듣고 공부한 글입니다.
1. 아핀 공간이 필요한 이유
이동 변환의 문제점
컴퓨터 그래픽스에서 중요한 기능 중 하나가 바로 이동 기능이지만, 선형 변환 개념으로는 이러한 이동을 구현할 수가 없습니다. 선형 변환이라는 것은 항상 원점으로부터 출발해서 어디까지 이어지는 지에 대한 화살표 개념이기 때문이죠. 이러한 이유로, 선형 변환을 통해 다음과 같이 기저 벡터를 원점으로부터 분리해 이동시킬 수는 없는 노릇입니다.

행렬의 관점으로 본다면, 다음과 같은 행렬은 존재하지 않는 것이죠.
밀기 변환의 활용
하지만, 밀기 변환을 활용하면 선형 변환의 형태로 이동을 구현하는 것이 가능해집니다. 밀기 변환은 1)한쪽 축은 그대로 둔 상태에서, 2)다른 축을 밀어내는 변환을 의미합니다. 원점에는 그대로 속해 있으므로 선형 변환이지요.

여기에서 일단

먼저, 원래 공간에 있는

만약

이것을 좀 더 일반화 해보면
즉, 2차원 공간에 대한 선형 변환을 수행하고, 이에 대한 결과물에서 1차원만 활용한다는 개념으로 접근하면, 선형성을 유지하면서 원하는 이동 변환을 구할 수 있게 되는 것입니다.
위에서 살펴 본
평면의 이동 변환
위에서 살펴 본 내용을 응용하여 3차원 공간에서 평면(2차원)을 밀면, 이동을 구현할 수 있습니다.

여기에서도
위와 같이 계산 후, 사용하지 않는 요소(위에선 세 번째
2. 아핀 변환(Affine transformation)
"점을 만들어내는 새로운 이동 변환"
위에서 했던 것처럼, 한 차원 공간을 높여서 진행하는 변환 작업을 수행해주면 이동, 회전, 크기 변환 또한 직접 선형 변환의 형태로 구현할 수 있게 됩니다. 이것을 아핀 변환(Affine transformation)이라고 합니다.
기존에 사용했던 회전(R), 크기(S) 변환은 크기가 2인 정방 행렬이었으므로, 이 또한 인위적으로 한 차원 늘려서 선형 변환의 형태로 구성할 수 있습니다.
이렇게 모든 선형 변환을 크기가 3인 변환으로 맞춰주게 되면, 행렬 곱 연산을 통해 연산량을 줄일 수 있는 장점을 그대로 가져갈 수 있습니다. 자주 사용되는 아핀 변환들은 다음과 같이 게임 제작에서 필수적으로 사용되는 변환들입니다.
- 이동 (Translation)
- 크기 (Scale)
- 회전 (Rotation)
3. 아핀 공간의 요소(Affine Space Elements)
선형 변환으로는 이동을 구현할 수 없어 밀기 변환을 응용하여 이동을 구현하였고, 좀 더 확장하여 크기와 회전까지 선형 변환 형태로 구성할 수 있게 하는 아핀 변환까지 알아보았습니다. 이러한 아핀 변환을 통해 변환된 공간을 아핀 공간(Affine Space)이라 부르는데, 이는 어떻게 구성되어 있을까요?
점(Point)
아핀 변환을 적용하려면 실제 이동시키는 공간보다 한 차원 더 높은 공간이 형성되어야 합니다. 예를 들어, 평면 이동을 위해서는 다음과 같은 3차원 공간이 형성되어야 하겠지요.
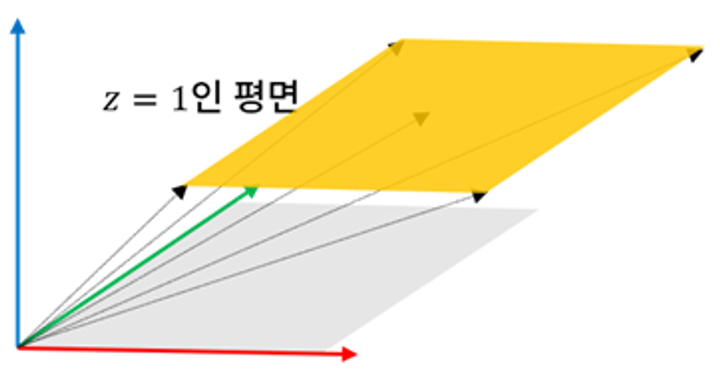
하지만 위와 같이 형성된 공간을 모두 사용하는 것은 아니고, 실제로 이동 가능한 공간이 따로 존재합니다. 평면 이동이기에 2차원의 관점에서 보면, 위 그림에선 노란색 영역이 해당 공간으로 간주할 수 있습니다.
그리고 아핀 변환을 위해 구성했던
- 1차원 공간의 점 :
- 2차원 공간의 점 :
- 3차원 공간의 점 :
이동 벡터(변위 벡터)
아핀 공간의 점에 대해서 알아보았는데, 그렇다면 이러한 아핀 공간의 새로운 점을 생성하는 생성 시스템이 필요할 겁니다. 이를 위해선 점과 점이 대응하는 관계에 대해서 무언가 만들 필요가 있습니다.
이때 사용하는 것이 아핀 공간에서의 이동 벡터(변위 벡터)입니다. 즉, 점의 대응 관계를 나타내기 위해서 사용하는 아핀 공간을 둘러싼 벡터 공간의 원소라고 볼 수 있죠.
이러한 이동 벡터를 점에 더하면 다른 벡터를 생성할 수 있게 됩니다. 다음은 점
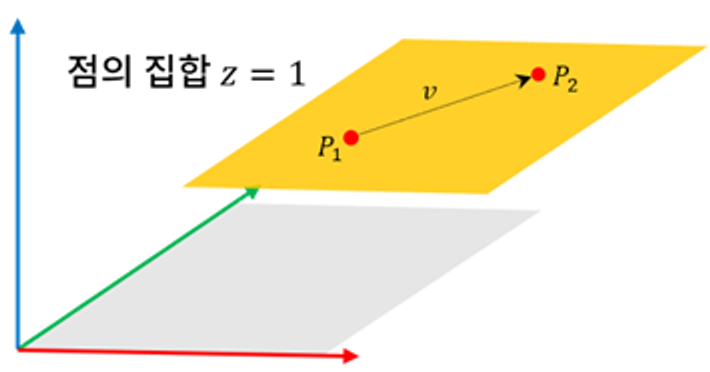
여기서 중요한 내용이 있는데, 아핀 공간의 점의 마지막 차원의 값은 항상 1이므로, 이동 벡터가 이 마지막 차원의 값에 영향을 주어서는 안 됩니다. 만약 영향을 주게 되면, 우리가 이동할 수 있는 평면 공간을 지정한 아핀 공간의 규칙을 깨기 때문이죠.
따라서, 이동 벡터들의 경우에는 마지막 차원의 값을 항상 0의 값을 가져야 합니다.
- 1차원 공간의 이동 벡터 :
- 2차원 공간의 이동 벡터 :
- 3차원 공간의 이동 벡터 :
여기까지 점과 이동 벡터에 대해 알아보았는데, 한 문장으로 요약하면 다음과 같이 할 수 있습니다.
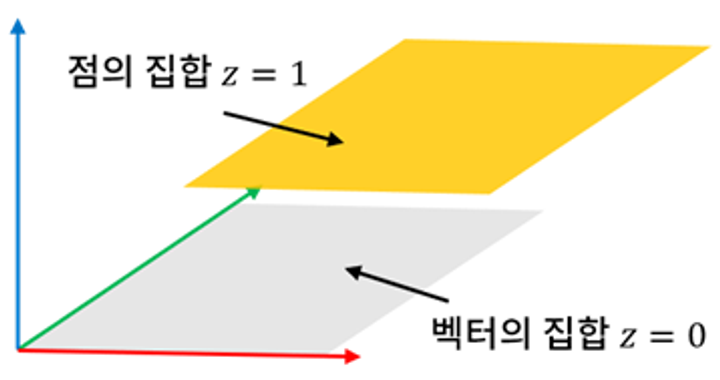
- 점 : 물체의 시각적 표현을 위한 위치 정보. 이동시킬 수 있는 이동 대상.
마지막 차원의 영역이 1인 공간 - 이동 벡터 : 점을 같은 공간 내에서 이동시키는 무형의 매개체 힘 (물리학의 벡터 개념과 유사)
마지막 차원의 영역이 0인 공간
4. 아핀 공간의 규칙 및 의의
아핀 공간의 규칙
아핀 공간에서 점과 벡터에 대한 규칙은 다음과 같습니다. 예전에 Unity로 게임 프로그래밍을 할 때, 벡터와 관련해서 계산하는 부분이 이해가 잘 안 된 적이 있었는데, 아핀 공간의 개념을 깨달으니 왜 그랬는지 이해가 되네요.
- 점 + 벡터 = 점 ( 마지막 차원 : 1 + 0 = 1 )
- 점 - 점 = 벡터 ( 마지막 차원 : 1 - 1 = 0 )
- 벡터 + 벡터 = 벡터 ( 마지막 차원 : 0 + 0 = 0 )
- 점 + 점 = 사용 불가 ( 마지막 차원 : 1 + 1 = 2 이므로, 아핀 공간을 벗어남. 원하는대로 이동 불가)
아핀 공간의 의의
아핀 공간은 기존 벡터 공간보다 한 차원 더 높은 공간을 의미하죠. 이 아핀 공간을 활용해 선형 변환으로 이동을 구현하고, 이 공간 위에서 캐릭터가 움직이고 탐험 가능한 월드 공간의 기반이 만들어지게 됩니다. 월드 공간 위에서 배치하는 물체는 아핀 공간의 점으로 구성되고, 해당 물체의 움직임은 이동 벡터를 활용해 구현하죠.
'Computer Sciences > Game Mathemathics' 카테고리의 다른 글
| [게임 수학] #12 | 직선(Line) (2) | 2023.11.26 |
|---|---|
| [게임 수학] #11 | 내적(Dot Product) (1) | 2023.11.25 |
| [게임 수학] #9 | 역행렬(Inverse Matrix) (1) | 2023.11.23 |
| [게임 수학] #8 | 행렬(Matrix) (0) | 2023.11.16 |
| [게임 수학] #7 | 선형성(Linearity) (0) | 2022.07.28 |