[게임 수학] #12 | 직선(Line)

인프런 <게임 엔진을 지탱하는 게임수학, 이득우 교수님> 강의를 듣고 공부한 글입니다.

 

 

1. 아핀 조합(Affine Combination)

이전에 아핀 공간에는 점과 이동 벡터가 존재하고, 점 + 점 연산은 불가능하다고 했었습니다. 하지만, 스칼라 값을 앞에 보조로 사용하여 곱하면 점 + 점 연산이 가능해집니다.

 

$$ a\cdot P_1 +b\cdot P_2 = ? $$

 

\( P_1, \ P_2 \) 가 2차원의 점이라고 가정할 경우, 위 조합식은 다음과 같이 전개됩니다.

 

$$ a(x_1, y_1, 1) + b(x_2, y_2, 1) = (ax_1+bx_2, \ ay_1 +by_2, \ a + b) $$

 

이때, 아핀 공간이므로 마지막 차원의 값이 반드시 1이 되어야 점이 될 수 있습니다. 즉, \( a + b = 1 \) 이 되어야 가능하다는 말이지요. 이를 원래 식에 대입하면 다음 식을 만들 수 있습니다.

 

$$ P(a) = a \cdot P_1 + (1-a) \cdot P_2 $$

 

위 식을 통해 만들어지는 결과는 점을 보장해주며, \(a\) 의 값에 따라 무수히 많은 점을 만들어 낼 수 있습니다. 이와 같이, 스칼라 값을 보조로 사용하여 기존에 불가능했던 점 + 점 연산을 가능하게 만들어, 새로운 점을 만들어내는 식을 아핀 조합(Affine Combination)이라고 합니다.

 

$$ \sum_{i = 0} ^n c_i \cdot P_i $$

$$ \mathrm{단,} \ \sum_{i=0}^n c_i = 1 $$

 

 

아핀 조합에 따라 생성된 점이 같은 선상에 있는지 어떻게 증명하는가?

위에서 아핀 조합에 대한 공식(\( P(a) = a \cdot P_1 + (1-a) \cdot P_2 \))을 알아보았고, \(a\) 값에 따라 점을 생성할 수 있다고 하였습니다. 그리고, 그 점들은 다음과 같습니다.

• \(a = 1\) 이라면, 점 \(P_1\)
• \(a = 0\) 이라면, 점 \(P_2\)
• \(0 < a < 1 \) 이라면, 점 \(P_1\) 과 점 \(P_2\) 사이에 있는 점
• \(a > 1 \) 이라면 점 \(P_1\)보다 바깥, \(a < 0\) 이라면 점 \(P_2\) 보다 바깥에 있는 점 

 

a 값에 따른 점의 위치

 

이러한 방식에 따라, \(a\) 의 값을 좀 더 촘촘하게 하면 기다란 선이 나타나게 됩니다.

 

 

이렇게 생성된 점들이 같은 선상에 있는지 증명해 보겠습니다. 먼저, 아핀 조합의 공식은 다음과 같았습니다.

 

$$ P' = aP_1 + (1-a)P_2 $$

 

위 식은 다음과 같이 작성할 수도 있습니다.

 

$$ P' - P_2 = a(P_1 - P_2) $$

 

이때, 아핀 공간에서 점 - 점은 벡터가 된다고 했었습니다.  \(P_1 - P_2 \) 를 하면, \(P_2\) 에서 \(P_1\) 을 향하는 벡터가 결과로 나오게 되죠. \( \vec{u} = P' - P_2\) , \( \vec{v} = P_1 - P_2 \) 라고 하고, 위 식을 다음과 같이 고쳐쓸 수 있습니다.

 

$$ \vec{u} = a\vec{v} $$

 

벡터 \(\vec{u}, \ \vec{v}\) 모두 점 \(P_2\) 에서 시작합니다.  그리고 벡터와 스칼라의 곱셈의 결과는 같은 기울기 선상에 있는 벡터로 결과가 만들어지죠? 그 말은, \(P_2 \rightarrow P' \) 으로 향하는 벡터(\(u\)) 와 \(P_2 \rightarrow P_1\) 으로 향하는 벡터(\(v\))의 기울기는 같다는 걸 의미합니다.

 

 

선의 종류

아핀 조합 공식에서 사용되는 스칼라 \(a\) 값의 범위에 따라 선의 종류가 나뉘게 됩니다.

• \( -\infty < a < \infty \)  :  직선(Line)
• \(0 \leq a < \infty \)  :  반직선(Ray)
• \(0 \leq a \leq 1 \)  :  선분(Segment)

 

선의 종류

 

 

---

2. 점의 표현

스크린 좌표계 (Screen Coordinate)

실제로 화면에 어떠한 점을 표현하기 위해선, 수학에서 가지고 있는 점의 개념을 그대로 적용하기는 어렵습니다. 디스플레이 해주는 모니터 화면의 하드웨어 사양에 맞춰서 변환을 해줘야 하기 때문이지요. 화면에 사용하는 스크린 좌표계(Screen Coordinate)는 수학에서 사용하는 데카르트 좌표계와 달리, 왼쪽 상단에서 오른쪽 하단으로 쭉 이어진 형태로 구성되어 있습니다. 그리고, 해상도라고 하는 크기에 따라 \((0, 0)\) 에서부터 정수로 하나씩 증가하는 특징을 가지고 있습니다.

 

예를 들어, 해상도가 \( 800 \times 600 \) 이라면 다음과 같이 구성되겠습니다.

 

스크린 좌표계

 

이러한 스크린 좌표계를 이루는 각각의 사각형 단위들을 픽셀(Pixel)이라고 부릅니다. 중요한 것은 이러한 스크린 좌표계가 정수 단위로 이루어져 있다는 점입니다. 이것은 결국에 우리가 사용하는 데카르트 좌표계의 실수 집합을 스크린 좌표계의 정수 값으로 변환하는 작업을 거쳐줘야 한다는 것이죠.

 

 

픽셀화 (Rasterization)

실제로 구현하는 단계에서, 어떤 벡터의 값을 화면의 픽셀로 변환해 찍는 작업을 픽셀화(Rasterization)라고 합니다. 수학적으로 지정한 물체의 형상을 몇 개의 픽셀들로 구성되어 있고, 색상은 어떤 걸로 구성할 지를 정하게 됩니다.

 

픽셀화

 

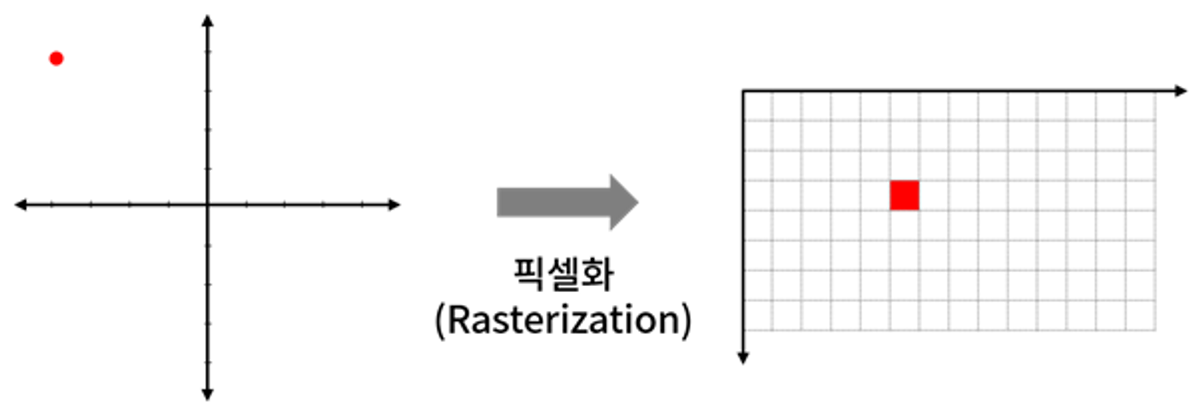
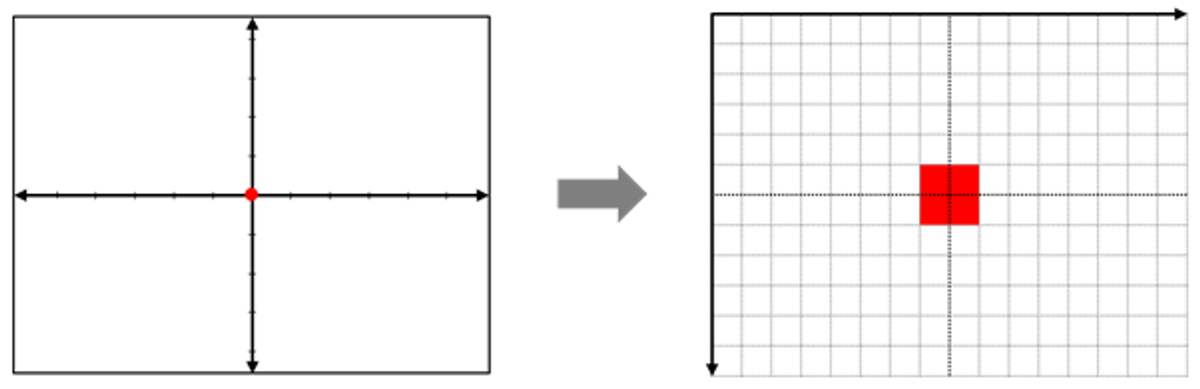
그런데, 만약 화면의 해상도가 짝수인 경우에는 중앙 픽셀을 표현하는 데에 한계가 발생합니다. 다음과 같이 4개의 픽셀들 중 하나를 골라야 하는 애매한 상황이 발생하죠. 이 경우에는 지정된 규칙에 따라, 4개 중 하나의 픽셀을 선택하는 수 밖에 없습니다.

 

화면 해상도가 짝수일 경우 발생하는 문제

 

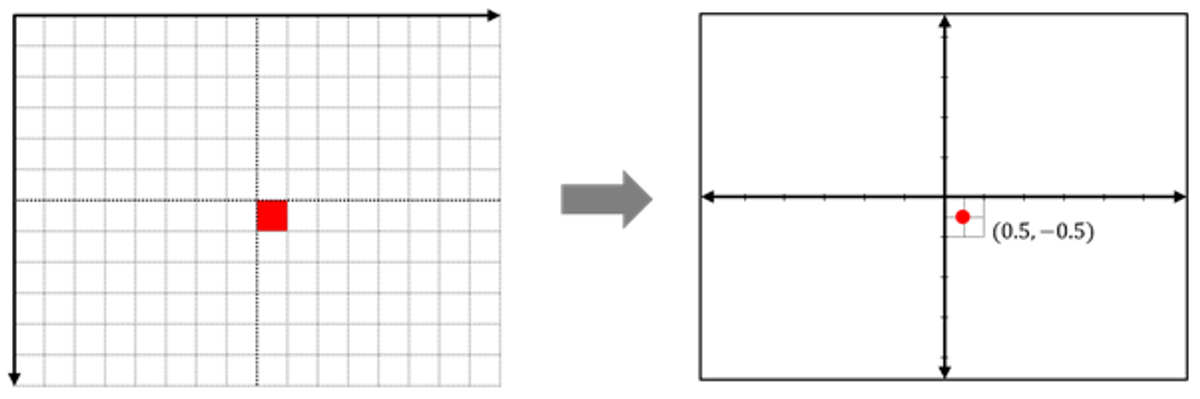
역으로 스크린 좌표계에서 데카르트 좌표계로 변환을 할 때에도 규칙을 지정해, 픽셀 영역 내에서 하나의 대표값을 추출해야 합니다. 다음 그림은 픽셀의 중앙값을 통해 벡터를 뽑아, 데카르트 좌표계로 변환하는 모습입니다.

 

중앙값을 이용한 스크린 좌표계에서 데카르트 좌표계로 변환

 

 

---

3. 선 그리기 알고리즘

수학적으로 설계한 공식(\( L(a) = a \cdot P_1 + (1-a) \cdot P_2 \))을 통해 선을 그리고, 거기에 픽셀을 맞출 수도 있겠지만 이는 어려운 점이 많습니다. \(a\) 의 값을 0.01이든 0.001이든 정밀하게 올릴 때, 이 정밀도는 기울기에 따라 달라질 것이고, 정밀도가 높아짐에 따라 컴퓨터 연산량이 많아져 부하가 심해집니다. 그래서, 이러한 선을 효과적으로 그릴 수 있는 방법으로 브레젠험 알고리즘이 있습니다.

 

브레젠험 직선 알고리즘 (Bresenham's Line Algorithm)

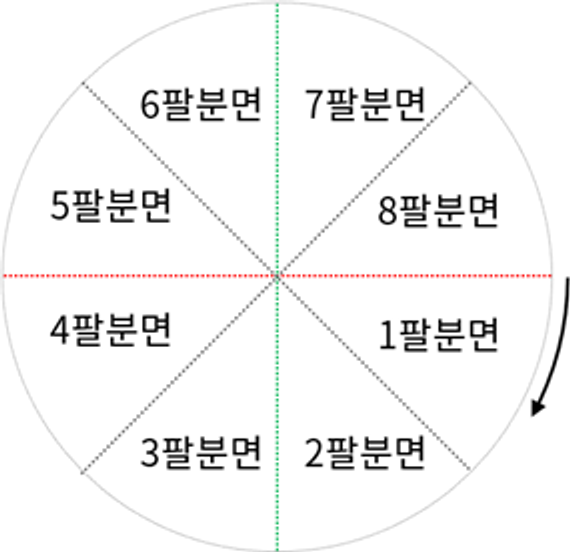
중점(Mid-point) 알고리즘이라고도 하며, 스크린 좌표계가 정수로만 이루어져 있기 때문에 정수 연산만을 사용한다는 내용을 기반으로 하는 알고리즘입니다. 브레젠험 알고리즘은 화면을 8등분하고 1 ~ 8(Octant)로 나눕니다.

 

 

우리가 흔히 아는 직선의 방정식은 다음과 같죠.

 

$$ y = ax + b $$

 

정수로 된 스크린 좌표계에서 두 점 \( P_1(x_0, \ y_0), \ P_2(x_1, \ y_1)\) 가 주어지면, 다음 정보를 얻을 수 있습니다.

• 너비(\(w\))  :  \( x_1 - x_0 \)
• 높이(\(h\))  :  \( y_1 - y_0 \)
• 시작점의 좌표 \((x_0, \ y_0)\), 끝 점의 좌표 \((x_1, \ y_1)\)

 

 

기울기 \(a = \frac{\Delta y}{\Delta x} = \frac{h}{w} \) 가 됩니다. 이렇게 구한 \(a\) 와 시작점 좌표 \( (x_0, \ y_0) \) 를 \( y = ax + b \) 에 대입하면, \(b\) 를 구할 수 있습니다.

 

$$ y_0 = \frac{h}{w}x_0 + b $$

$$ \therefore b = y_0 - \frac{h}{w}x_0 $$

 

이렇게 구한 \(a, \ b\) 를 원래 직선의 방정식에 넣어, 다음과 같은 식을 얻을 수 있습니다.

 

$$ y = \frac{h}{w}x + y_0 - \frac{h}{w}x_0 $$

 

 

브레젠험 알고리즘 예시 시나리오

시작점 \((x_0, \ y_0)\) 와 끝 점 \((x_1, \ y_1)\) 이 주어지고 기울기를 구해봤을 때, 이 직선이 1팔분면 방향에 해당한다고 가정해 봅시다. 1팔분면 방향이므로, 선분은 오른쪽 아래 방향으로 나아갈 것입니다.

 

그렇다면, 시작점 이후 다음으로 찍을 점이 시작점에서 오른쪽으로 평행 이동하는지, 아니면 오른쪽 한칸 아래로 내려가는지를 판별해야 합니다. 이는 중점 값을 보고 판단할 수 있습니다. 

 

오른쪽 점과 오른쪽 아래 점 중 무엇을 택해야 할까요?

 

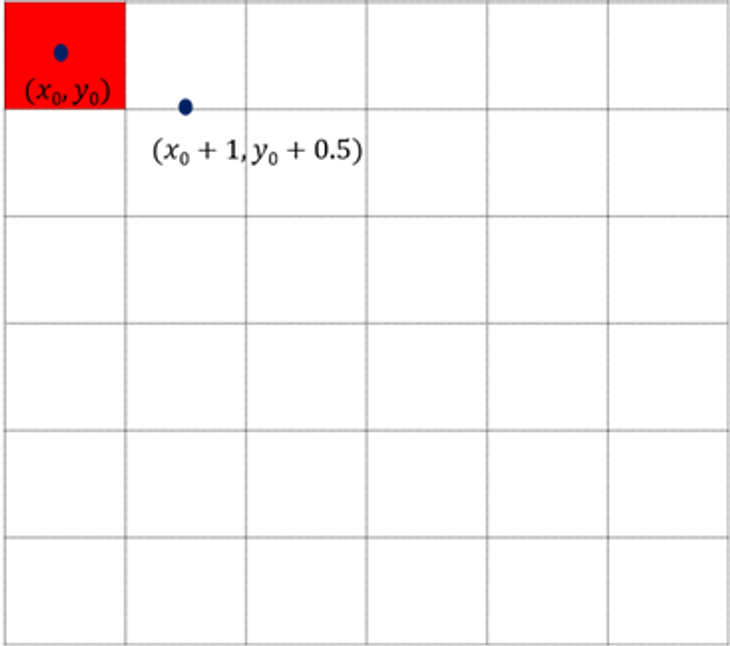
위에서 구했던 직선 방정식에서 \(x = x_0 + 1\) 을 대입한 값 \(y\) 가 \( y_0 + 0.5 \) 보다 작다면, 오른쪽으로 평행 이동한 점을 선택하면 됩니다. 그게 아니라면, 한칸 아래로 내려가면 되겠지요.

 

수식으로 나타내면 다음과 같습니다.

 

$$ y = \frac{h}{w}(x_0 + 1) + y_0 - \frac{h}{w}x_0 = \frac{h}{w} + y_0 $$

 

즉, \( \frac{h}{w} + y_0 < y_0 + 0.5 \) 이면 오른쪽으로 한 칸 평행이동, 아니라면 오른쪽 아래로 한 칸 이동합니다. 위 부등식은 다음과 같이 단순화 시킬 수 있습니다.

 

$$ \frac{h}{w} - 0.5 < 0 $$

$$ \rightarrow \ 2w(\frac{h}{w} - 0.5) < 0 \cdot 2w $$

$$ \rightarrow \ 2h - w < 0 $$

 

 

이를 통해, 우리는 판별식 \(2h - w < 0 \) 을 얻게 되었습니다. 계속해서 \(x\) 값을 1씩 증가시켜며, 다음 중점 값에 대해 판별식 값의 변화를 살펴보면 다음과 같은 일정한 패턴을 보이는 것을 확인할 수 있습니다.

• 평행 이동할 경우, \(2h\) 만큼 증가
• 아래로 내려갈 경우, \(2h - 2w\) 만큼 증가

 

 

즉, 이를 통해 다음과 같은 알고리즘 순서도를 생각할 수 있습니다.

1. 최초 판별식을 구하고 시작점을 찍는다.
2. 판별식 \(<\) 0 이라면 평행 이동이므로, \(x\) 값을 1 증가시키고, 판별식에 \(2h\) 를 더한다.
3. 판별식 \(\geq\) 0 이라면 오른쪽 한 칸 아래로 이동이다.
   이에 따라, \(x, \ y\) 값을 1씩 증가시키고, 판별식에 \(2h - 2w\)를 더한다.
4. 점을 찍고, 끝 점에 도달할 때까지 2 ~ 3번 과정을 반복한다.

 

 

나머지 팔분면에서는 어떻게 진행하는가?

 

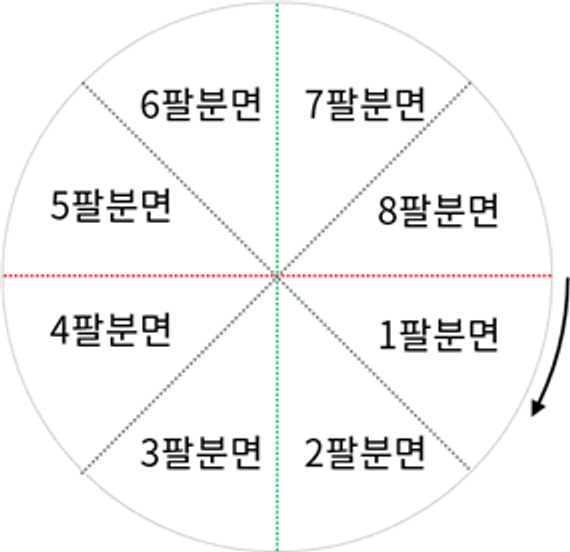
위에서 1팔분면에 대한 시나리오를 확인해 봤는데, 그럼 나머지 팔분면 방향에 대해서는 어떻게 처리할까요?

 

기울기가 0 ~ 45도로 한정되어 가파르지 않은 1, 4, 5, 8팔분면들은 사실상 매커니즘이 거의 동일합니다. 1, 8팔분면은 \(x\) 값은 그대로 증가시키고, \(y\) 값을 증가시키냐, 감소시키냐에 대한 차이일 뿐이죠. 1팔분면에선 \(y\) 값이 점차 증가했지만, 8팔분면에선 \(y\) 값이 점차 감소하겠지요. 4, 5팔분면도 \(x\) 가 감소한다는 것 외에는 똑같습니다.

 

그에 반해, 기울기가 45도 ~ 90도로 한정되어 가파른 2, 3, 6, 7팔분면들은 관점을 조금 바꿔서 적용해줘야 합니다. \(x\) 가 변하는 것이 아닌 \(y\) 가 변하는 관점으로요. \(y\) 축을 기준으로 보게 되면 2, 3, 6, 7팔분면 기울기들도 다시 0 ~ 45도로 완만한 경사의 기울기가 되기 때문이지요. 따라서, \(x\) 와 \(y\) 를 바꾼 상태로 동일하게 알고리즘을 적용하면 되며, 판별식 또한 너비와 높이를 바꿔서 적용해주면 됩니다.