2023. 11. 25. 21:37ㆍComputer Sciences/Game Mathemathics
인프런 <게임 엔진을 지탱하는 게임수학, 이득우 교수님> 강의를 듣고 공부한 글입니다.
1. 벡터의 내적(Dot Product)이란?
벡터에는 벡터와 벡터의 덧셈, 벡터와 스칼라의 곱셈과 같은 연산을 통해 새로운 벡터를 생성해낼 수 있는 시스템이 존재합니다. 하지만 이것만으로는 부족하여 좀 더 응용할 수 있는 연산들을 수학자들이 추가하게 되었는데, 그것이 바로 벡터의 내적과 외적입니다. 여기에서는 내적에 대해서만 알아보도록 하겠습니다.
내적 연산
벡터의 내적 연산은 벡터 내에서 같은 요소들끼리 서로 곱한 후, 더해주는 연산입니다. 예를 들어, \(v_1 = (a, b) \) 와 \(v_2 = (c, d) \) 와 같은 2차원 벡터를 서로 내적한다고 하면, 두 벡터의 대응되는 각 요소인 \(a\) 와 \(c\) , 그리고 \(b\) 와 \(d\) 를 다음과 같이 서로 곱한 후 더해주면 됩니다.
*벡터의 내적 기호는 \(\cdot\) 으로 표기합니다.
$$ (a,b)\cdot (c,d)=ac+bd $$
벡터의 각 요소들을 곱한 후 더해주기 때문에, 내적의 결과는 항상 스칼라 값인 것을 알 수 있습니다. 그렇다면, 벡터의 내적은 교환 법칙, 결합 법칙, 분배 법칙을 각각 만족할까요?
교환 법칙 👉🏻 성립
내적은 덧셈과 곱셈으로 이루어진 연산이기 때문에 체의 특성상, 교환 법칙이 성립합니다.
$$ \vec{u}\cdot \vec{v}=\vec{v}\cdot \vec{u} $$
$$ (a,b)\cdot (c,d)= ac+bd $$
$$ (c,d)\cdot (a,b)=ca+db $$
$$ \therefore (a,b)\cdot (c,d)=(c,d)\cdot (a,b) $$
결합 법칙 👉🏻 성립하지 않음
내적의 결과는 스칼라가 나오게 되고, 이것과 다른 벡터를 곱한다는 것은 항상 같은 결과가 나오리라고 보장할 수 없습니다. 따라서, 내적에 대한 결합 법칙은 성립하지 않습니다.
$$ (\vec{u}\cdot \vec{v})\cdot \vec{w}\ne\vec{u}\cdot (\vec{v}\cdot \vec{w}) $$
분배 법칙 👉🏻 성립
벡터와 벡터를 더하고 내적을 진행해도 스칼라 값이 되고, 각각의 벡터들을 내적해도 스칼라 값이 되므로 분배 법칙이 성립한다고 할 수 있겠습니다.
$$ \vec{u}\cdot (\vec{v}+\vec{w})=\vec{u}\cdot \vec{v} + \vec{u}\cdot \vec{w} $$
내적에 대한 유용한 식
자기 자신의 벡터와 내적하면, 벡터의 크기의 제곱값이 항상 나오게 됩니다. 예를 들어, \(v = (x, y) \) 라는 벡터가 있고, 자기 자신에 대한 내적 \((x, y) \cdot (x, y) \) 을 진행하면 결과는 다음과 같습니다.
$$ v \cdot v = (x, y) \cdot (x, y) = x^2 + y^2 $$
이 값은 벡터의 크기 \( | v | = \sqrt{x^2 + y^2}\) 을 제곱한 것과 같습니다. 이러한 내용에 기반하여, 다음과 같은 식을 유도할 수 있습니다.
$$ (u+v)\cdot (u+v) = u\cdot u+v\cdot v+2(u\cdot v) = |u|^2+|v|^2+2(u\cdot v) $$
2. 벡터의 내적이 가지고 있는 성질
벡터 내적의 코사인 공식
벡터의 내적은 코사인(cos) 함수와 밀접한 관계가 있습니다. 다음 공식은 게임을 제작할 때, 가장 많이 사용되는 중요한 공식입니다.
$$ a \cdot b = |a||b|cos\theta $$
즉, 어떠한 벡터 \(a\) 와 \(b\) 를 내적한 결과는 두 벡터의 각각의 크기에다가 그 사잇각(\(\theta\)) 을 곱한 것과 같다고 해석할 수 있습니다. 어떻게 그런 결과가 나오는 것인지 한 번 알아보도록 하죠.

점 \(B\)를 원점에 두고, 각 변을 벡터로 설정한다고 했을 때, 각 점의 위치는 다음과 같습니다.
- \(B = (0, 0) \) 👉🏻 원점
- \(C = (|\vec{a}|, 0) \) 👉🏻 원점에서 \(x\) 축 방향으로 벡터 \(\vec{a}\) 의 크기만큼 떨어져 있으므로
- \(A = (|\vec{c}|cos\beta, |\vec{c}|sin\beta) \) 👉🏻 반지름이 \(r\) 인 원에서의 좌표값은 \((rcos\beta, rsin\beta)\)
여기서 벡터 \(\vec{b}\) 를 계산해 봅시다. 벡터 \(\vec{b}\) 는 점 \(A\) 에서 점 \(C\) 방향을 향하므로 \(C - A\) 가 됩니다.
$$ \vec{b} = (C - A) = (|\vec{a}| - |\vec{c}cos\beta|, \ 0 - |\vec{c}|sin\beta) $$
그런데, 우리는 위에서 벡터 자기 자신을 내적한 결과는 그 벡터의 크기를 제곱한 결과와 같다(\( \vec{b} \cdot \vec{b} = |\vec{b}|^2 \))는 것을 알아봤었습니다. 그럼, 우선 \(|\vec{b}|^2\) 을 먼저 구해보죠.
$$ |\vec{b}|^2 = (|\vec{a}| - |\vec{c}|cos\beta)^2 + (|\vec{c}|sin\beta)^2$$
$$ = |\vec{a}|^2 - 2|\vec{a}||\vec{c}|cos\beta + |\vec{c}|^2cos^2\beta + |\vec{c}|^2sin^2\beta $$
여기서, \( |\vec{c}|^2cos^2\beta + |\vec{c}|^2sin^2\beta = |\vec{c}|^2(cos^2\beta + sin^2\beta) = |\vec{c}|^2 \) 이므로 위의 식은 다음과 같이 정리할 수 있습니다.
$$ |\vec{b}|^2 = |\vec{a}|^2 -2|\vec{a}||\vec{c}|cos\beta + |\vec{c}|^2 $$
즉, 위의 식이 \( \vec{b} \cdot \vec{b}\) 과 같은 것이니 다음과 같이 쓸 수 있겠습니다.
$$ \vec{b} \cdot \vec{b} = |\vec{a}|^2 -2|\vec{a}||\vec{c}|cos\beta + |\vec{c}|^2 $$
여기서, \( \vec{b} \) 를 \( \vec{a}, \ \vec{c} \) 로 바꾸어 작성해 봅시다.
$$ \vec{b} \cdot \vec{b} = (\vec{a} - \vec{c}) \cdot (\vec{a} - \vec{c}) = (\vec{a}+(-\vec{c}))\cdot (\vec{a}+(-\vec{c}))$$
$$ = |\vec{a}|^2+|\vec{c}|^2-2\vec{a}\cdot \vec{c} $$
그럼 이제 이 내용들을 가지고 결론을 내봅시다.
$$ \vec{b} \cdot \vec{b} = |\vec{b}|^2 $$
$$ \rightarrow \ |\vec{a}|^2+|\vec{c}|^2-2\vec{a}\cdot \vec{c} = |\vec{a}|^2 -2|\vec{a}||\vec{c}|cos\beta + |\vec{c}|^2 $$
$$ \rightarrow \ -2\vec{a} \cdot \vec{c} = -2|\vec{a}||\vec{c}|cos\beta $$
$$ \therefore \vec{a} \cdot \vec{c} = |\vec{a}||\vec{c}|cos\beta $$
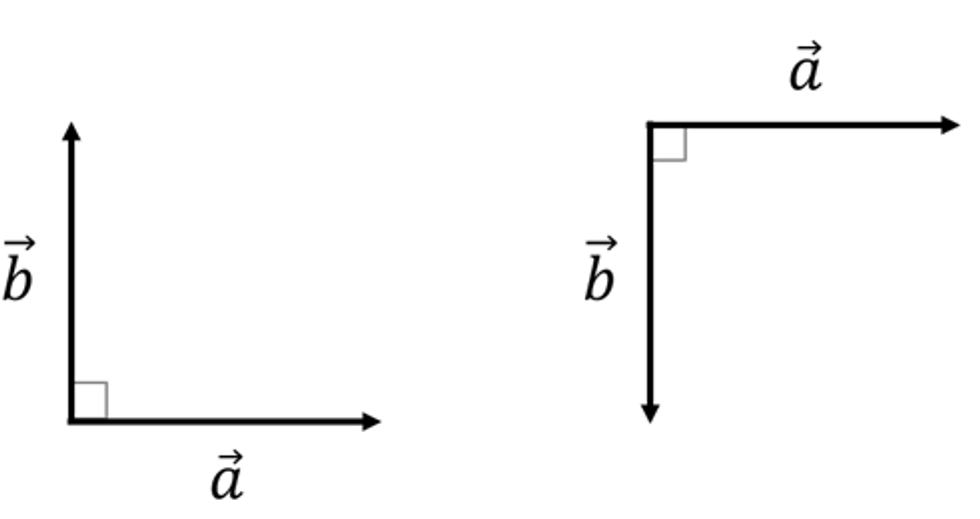
벡터 내적의 직교성 판별
위에서 코사인 함수와 관련된 벡터 내적 공식 증명을 진행하였습니다. 이렇게 구한 공식을 응용할 수 있는 대표적인 예시들 중 하나는 두 벡터의 직교성을 판별입니다. 벡터의 크기가 0이 아닐 때, 내적의 결과가 0이 나오는 경우는 \(cos\beta = 0\) 일 때 밖에 없습니다. 즉, \( \beta = 90\) 일 때이지요.
강체 변환(Rigid Transformation)
물체의 모습이 변형되지 않는 최소 단위를 이야기 하는 것이며, 결국에는 어떤 물체가 변환이 일어났을 때 그 모습이 그대로 유지되는 것을 말합니다. 이러한 강체 변환이 적용되기 위한 조건들은 다음과 같습니다.
- 공간을 구성하는 모든 기저 벡터의 크기가 1이어야 한다.
- 모든 기저 벡터가 서로 직교하고 있어야 한다. 👉🏻 원래 공간의 벡터들이 서로 직교하고 있기 때문
- 선형 변환의 행렬식 값이 1이어야 한다.
이를 만족하는 대표적인 변환은 회전 변환입니다.
$$ R = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} $$
3. 벡터 내적의 활용
1) 앞 뒤 판별
벡터 내적의 코사인 공식을 활용하여 목표물이 현재 내 앞에 있는지, 뒤에 있는지를 파악할 수 있습니다. 내 정면 벡터 \(\vec{a}\) 와 적을 가리키는 벡터 \(\vec{b}\) 가 있다면, 이 두 벡터의 내적 결과가 양수라면 앞에, 음수라면 뒤에 있음을 의미합니다.

코사인은 (-90º, 90º) 범위에 있으면 항상 양의 값을 가진다는 성질을 활용하였기에 위와 같은 판별을 할 수 있는 것이지요.
2) 시야 판별
1)에서 살펴 본 내용을 응용하여 적이 내 시야 내에 들어와 있는지 판별하는 데에도 벡터의 내적을 사용할 수 있습니다.

각 \(\alpha \) 가 시야각의 절반 값인 \( \frac{\beta}{2}\) 보다 작다면, 목표물은 시야각 내에 위치한다고 볼 수 있습니다. 이를 판별하는 데 진행하는 과정은 다음과 같습니다.
- 게임에서 시야각이 변하는 일은 잘 없기에, \( cos\frac{\beta}{2}\) 값을 미리 구해 저장해둔다.
- 시선 벡터와 목표물로 향하는 벡터의 크기를 1로 정규화한다.
그렇다면, 두 벡터의 내적은 \(cos\alpha\) 가 된다. - 코사인 함수는 (0º, 180º) 범위에서 각이 증가할수록 값이 감소한다.
- ∵ \( cos\frac{\beta}{2} < cos\alpha\) 면 시야 범위 내에 있다고 파악한다.
3) 음영 계산
3차원 컴퓨터 그래픽에서 빛을 가지고 있는 방향에 따라 명암을 지정할 때, 벡터의 내적이 유용하게 사용됩니다. 물체의 표면 방향과 광원 방향의 사잇각이 작을수록 빛이 많이 들어오고, 클수록 빛이 적게 들어오게 됩니다.

표면의 방향 벡터를 \(\vec{N}\) , 표면에서 광원을 향하는 벡터를 \(\vec{L}\) 이라고 한다면, 이 두 벡터의 사잇각 \(\theta\) 이 클수록 빛이 적게 들어오고, 작을수록 빛이 많이 들어온다는 소리이지요. 즉, 코사인 값에 비례하여 빛이 들어옵니다.
이와 관련된 셰이더 기본 조명 공식으로, 램버트 코사인 법칙(\(N \cdot L \))이 있습니다.
물체 표면이 반사하는 빛의 휘도(Luminance)는 표면 방향과 광원 방향의 사잇각의 코사인 값에 비례한다.
즉, \(\vec{N}\) 과 정규화 한 \(\vec{L}\) 을 내적하여, 단순히 \(cos\theta\) 값에 비례하여 빛의 양을 조절하면 된다는 의미이지요. Unity 엔진에서 이 공식을 사용하여 만든 가장 간단한 셰이더를 Diffuse Shader라고 이야기 합니다.
4) 투영 벡터
어떤 두 개의 벡터가 있고, 이들 중 하나를 다른 하나의 벡터에 투영을 했을 때, 투영한 벡터의 크기 또는 값은 어떻게 되는지를 파악하는 공식입니다. 다음 그림에서 벡터 \(u\) 의 투영 벡터인 \(v'\) 는 \(v\) 와 크기만 다를 뿐, 같은 방향을 가집니다.

이때, 투영된 벡터 \(v'\) 는 다음과 같이 구할 수 있습니다.
- 같은 방향의 벡터 \(v\)를 정규화 한 벡터 \(\hat{v}\) 를 구한다.
- \(\hat{v} \) 에 벡터 \(v'\) 의 크기를 곱해준다.

\(\hat{v} = \frac{v}{|v|} \) 로 구할 수 있고, 코사인 삼각비 공식(\(\frac{밑변}{빗변}\))를 사용하여 \( |v'| = |u|cos\theta \) 로 구할 수 있습니다.
이제 거의 다 왔는데, \(cos\theta\) 값만 알면 \(v'\) 을 알 수 있습니다. \(cos\theta\) 는 내적을 통해 알 수 있습니다.
$$ u \cdot v = |u||v|cos\theta $$
$$ \therefore cos\theta = \frac{u \cdot v}{|u||v|} $$
이제, 이를 대입하여 투영 벡터 \(v'\) 의 최종 식을 구할 수 있습니다.
$$ v' = \frac{(u \cdot v) \cdot v}{|v|^2} = \frac{(u \cdot v) \cdot v}{(v \cdot v)}$$
여기서 투영하려는 벡터의 크기(\(|v|\))가 1이라면, 다음과 같이 더 단순해집니다.
$$ v' = (u \cdot v) \cdot v $$
'Computer Sciences > Game Mathemathics' 카테고리의 다른 글
| [게임 수학] #13 | 삼각형(Triangle) (1) | 2023.11.27 |
|---|---|
| [게임 수학] #12 | 직선(Line) (2) | 2023.11.26 |
| [게임 수학] #10 | 아핀 공간(Affine Space) (1) | 2023.11.24 |
| [게임 수학] #9 | 역행렬(Inverse Matrix) (1) | 2023.11.23 |
| [게임 수학] #8 | 행렬(Matrix) (0) | 2023.11.16 |