[게임 수학] #20 | 원근 투영(Perspective Projection)

*인프런 <게임 엔진을 지탱하는 게임수학, 이득우 교수님> 강의를 듣고 공부한 글입니다.

 

 

1. 원근 투영 변환(Perspective Projection Transformation)

현실 세계의 모습을 담을 수 있는 "사진"

 

맛있는 음식이 나왔을 때, 카페에 가서 디저트와 음료를 시켰을 때 등등 일상 생활 속에서 우리는 많은 순간 카메라로 사진을 찍곤 합니다. 하지만, 현실 세계는 3차원이고 카메라로 찍게 되는 사진은 2차원인데 어떻게 우리가 이질감을 느끼지 않고 있는 사실 그대로 받아들일 수 있는 걸까요? 바로 원근감이 형성되었기 때문입니다.

 

이에 따라, 가상 세계를 만들고 있는 우리 또한 이 원근감을 형성해주는 작업을 해줘야 한다는 의미가 되며, 오늘은 이러한 작업에 대한 원근투영 변환을 알아보는 시간을 가지도록 하겠습니다.

 

 

원근 투영 변환의 원리

3차원 공간은 3개의 축이 서로 직교하는 형태의 공간입니다. 하지만 우리 눈은 이런 3차원 공간을 조금 다른 형태로 보고 있죠. 우리 눈이 바라보는 세계는 카메라처럼 한 점에서 출발해, 화각으로 쫙 펼쳐지는 형태로 구성되어 있습니다.

 

우리 눈이 보는 형태

 

화각으로 펼쳐진 공간 내에 있는 물체를 어떠한 평면에 담는 것이고, 우리는 그 평면을 보는 것이죠.

 

 

우리가 보는 이 평면은 우리의 눈(카메라)와의 거리에 따라 멀어질수록 커지고, 가까워질수록 작아질 겁니다. 이러한 평면들이 모인 집합이 바로 위와 같이 사각뿔 형태가 되겠지요. 여기서, 우리는 다음과 같은 개념을 적립할 수 있습니다.

• 투영 평면 : 화각으로 펼쳐진 공간 내 수많은 평면들이 모인 집합 중에서, 우리가 화면에 담을 평면
• 초점거리  : 카메라로부터 투영 평면까지의 거리

 

 

위에서 말한 내용을 옆에서 보면 다음과 같습니다.

 

 

화각(Field of View) 이 \(\theta\), 물체을 담을 투영 평면, 그리고 초점거리 \(d\) 가 정해져 있습니다. 이제 이러한 정보들을 가지고 어떻게 원근 투영을 구현할 지가 문제인데, 일반적으로 NDC(Normalized Device Coordinate)라는 방법을 많이 사용합니다.

 

 

NDC(Normalized Device Coordinate)

모니터의 스펙에 따라 달라지는 해상도를 고려해, 화면 크기를 정규화하여 관리하는 방법입니다. 텍스처에서도 텍스처 이미지의 크기에 상관없이 UV 좌표계를 (\(0, \ 0\))에서 (\(1, \ 1\))까지 지정했던 것과 동일하게, 투영하는 평면의 절반 크기가 항상 1이 되도록 지정하는 것이죠. 이것을 NDC 좌표계라고 부릅니다.

 

 

평면 절반의 길이가 1이 되면, [좌] 그림을 봤을 때 높이가 1인 직각삼각형이 2개가 만들어지게 됩니다. 정면에서 투영 평면을 보게 되면, [우] 그림과 같이 중앙 (\(0, \ 0\)) 으로부터 시작해 상하좌우로 최대 1만큼씩 떨어진 좌표계가 생기게 되죠. 이러한 평면에 투영시켜 표현되는 정점들의 좌표를 NDC라고 하는 것입니다.

 

1) 초점거리 구하기

화각은 우리가 설정하는 것이니 주어지고, 평면의 절반 길이가 1이라는 것도 주어졌습니다. 그럼 이제 이걸 토대로 초점거리 \(d\) 를 구해야 하는데요. 아까 위에서 봤던 직각삼각형을 활용해 구할 수 있습니다.

 

 

평면은 항상 절반 길이 1을 유지해야 하므로, 화각이 작아지면 그만큼 뒤로 밀려날 것이고, 화각이 커지면 앞으로 당겨질 겁니다. 또한, 화각 \(\frac{2}{\theta}\) 와 높이 1을 토대로 \(tan\) 를 계산하면, 초점거리 \(d\) 다음과 같이 구할 수 있습니다.

 

$$ d = \frac{1}{tan(\frac{2}{\theta})} $$

 

 

2) 뷰 공간의 점을 NDC 점으로 변환  👉🏻  답은 "삼각비"

뷰 공간의 점 \(P_{view}\) 에서 카메라를 향해 직선을 그었을 때, 투영 평면에 배치되는 점 \(P_{ndc}\) 를 구해야 합니다.

 

뷰 공간 -> 투영 평면

 

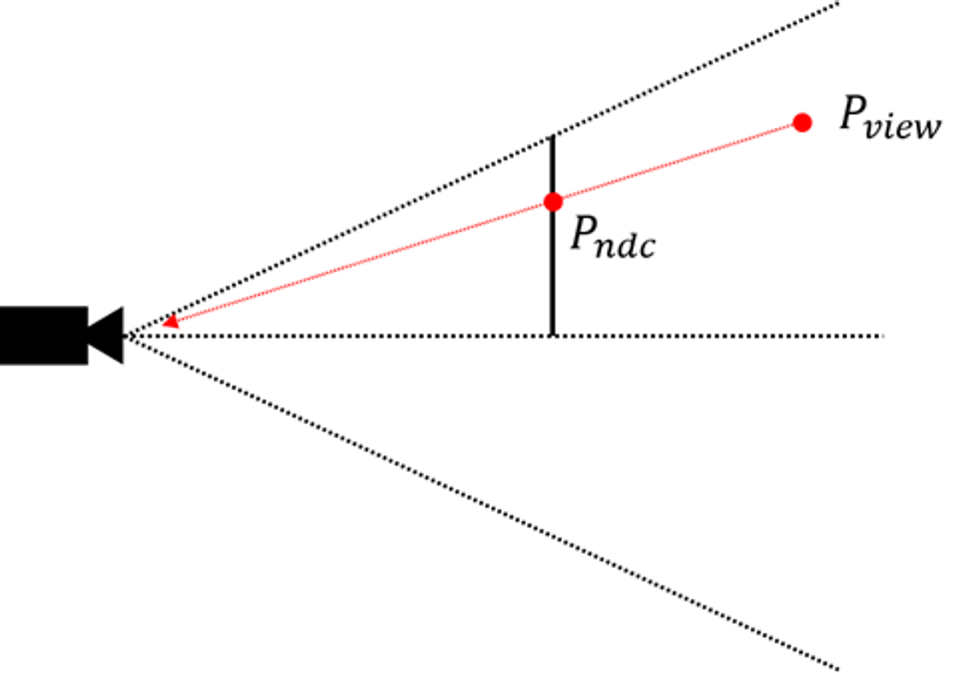
이러한 과정을 뷰 공간에 있는 점들에 대해 진행하고, 이렇게 구한 NDC 좌표계의 점들로 렌더링을 하면 원근감 있는 3차원 공간을 그릴 수 있게 됩니다. 우리는 이렇게 \(P_{view} \rightarrow P_{ndc} \) 로 변환을 해주는 행렬을 만드는 것이 목표죠.

 

그렇다면, 뷰 공간에 있는 점을 어떻게 NDC 좌표계로 변환할 수 있을까요? 이것은 삼각비를 활용해 해결할 수 있습니다.

먼저, NDC의 \(y\) 좌표를 구하기 위해 옆에서 바라본 모습을 한번 보죠.

 

삼각비

 

뷰 공간의 임의의 점 \(P_{view}\) 와 카메라로부터의 거리와 높이 값은 (\(0, \ v_y, \ v_z)\)으로 구할 수 있습니다. 그리고 카메라 관련 내용을 다룰 때, 물체와 카메라의 로컬축 방향이 달라지는 것을 방지하기 위해, 카메라가 오른손 좌표계 기준으로 \(-z\) 방향을 바라본다고 했구요.

 

그렇다면 우리가 알고있는 정보인 초점거리 \(d\), 카메라로부터 \(P_{view}\) 까지의 거리 \(-v_z\), \(P_{view}\) 의 높이 \(v_y\) 를 토대로 \(P_{ndc}\) 의 높이 값 \(n_y\) 를 삼각비로 알 수 있습니다.

 

$$ n_y : d = v_y : -v_z $$

$$ \therefore n_y = \frac{d \cdot v_y}{-v_z}$$ 

 

\(P_{ndc}\) 의 \(x\) 축 값인 \(n_x\) 또한 똑같이 구할 수 있습니다. \(y\) 축 값을 구할 땐 옆에서 바라봤지만, 이번에는 위에서 아래로 내려다보고, \(x\) 축 또한 \(y\) 축과 같은 시야각을 가지고 서로 직교하므로 동일하게 구할 수 있습니다.

 

$$ n_x = \frac{d \cdot v_x}{-v_z}$$

 

이를 통해, 투영된 최종 좌표는 다음과 같습니다.

 

$$ P_{ndc}=\left(\frac{d\cdot v_x}{{-v}_z},\frac{d\cdot v_y}{{-v}_z}\right)=-\frac{d}{v_z}(v_x,v_y) $$

 

 

3) 실제 해상도 화면으로 적용하기

이제 정규화 된 이 NDC 공간에서의 각 투영 좌표를 얻었으니, 실제로 화면 해상도에 맞출 때에는 해상도만큼 가로, 세로를 늘려서 계산하면 됩니다. 가령, \(800 \times 600\) 해상도에 표현해야 한다면, 가로와 세로 절반인 각각 400, 300씩 늘려주면 된다는 소리죠.

 

 

하지만 문제가 하나 있는데, NDC 공간은 가로와 세로가 동일한 길이이지만 대부분의 모니터 해상도들은 그렇지 않습니다. 따라서, 있는 그대로 확대하여 적용하게 된다면 다음과 같이 찌그러진 형태로 보이게 됩니다.

 

 

이를 방지하려면, 모니터 해상도의 종횡비를 NDC 공간에 반영해 모양을 찌그러트리고, 이를 실제 모니터에 늘려서 표현할 땐 온전한 모습으로 나오게끔 할 수 있습니다.

 

 

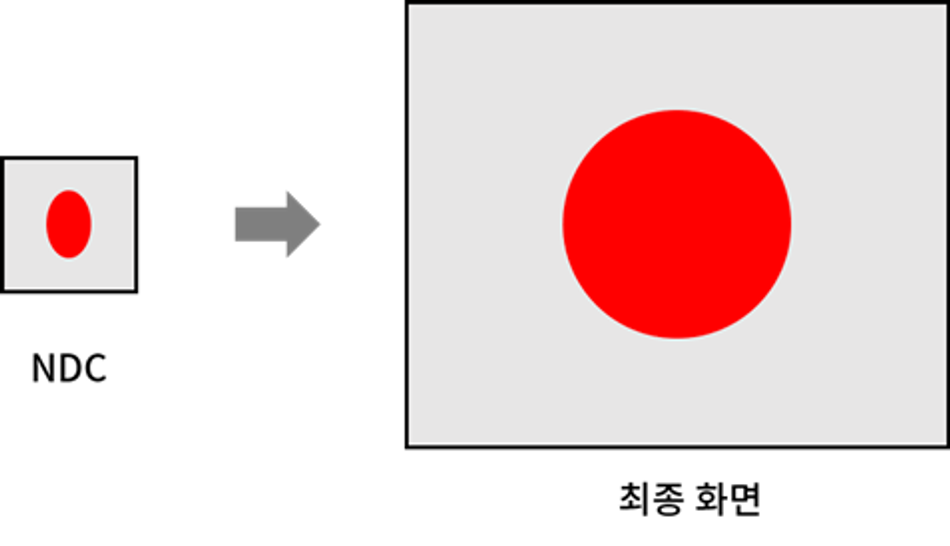
이러한 종횡비는 보통 세로를 기준으로 많이 하며, 이를 통해 구한 종횡비 \(a\) 는 다음과 같습니다.

 

$$ a = \mathrm{\frac{width}{height}}$$

 

이렇게 되면, 보통 세로가 가로 길이보다 짧기 때문에 \(a > 1\) 이 될 겁니다. 가로가 더 길기 때문에 가로로 더 많이 늘어날 것이므로 \(y\) 에 대한 부분은 딱히 사용하지 않고, \(x\) 에 대해서만 찌그러트릴 겁니다. 이를 위해, \(x\) 에 대해서만 종횡비 \(a\) 의 역수를 반영해 주는거죠.

 

$$ P_{ndc} = -\frac{d}{v_z}(\frac{v_x}{a}, \ v_y) $$

 

 

4) 투영 변환 행렬 구하기

위에서 구한 식 \(P_{ndc} = -\frac{d}{v_z}(\frac{v_x}{a}, \ v_y)\) 를 통해, 다음과 같은 투영 행렬을 생성할 수 있습니다.

 

$$ P\cdot\ v=\left[\begin{matrix}\frac{1}{a}\cdot\frac{d}{{-v}_z}&0&0\\0&\frac{d}{{-v}_z}&0\\0&0&1\\\end{matrix}\right]\left[\begin{matrix}v_x\\v_y\\v_z\\\end{matrix}\right] $$

 

하지만 위 행렬은 문제가 있습니다. 행렬 요소를 보면 \(-v_z\) 값을 사용하고 있는데, 이것은 뷰 공간에 있는 점마다 다릅니다. 즉, 뷰 좌표계의 값을 사용하고 있기 때문에 10만 개의 점을 변환한다고 가정하면 10만 개의 다른 행렬이 생성되어야 한다는 것이죠. 이것은 행렬을 사용하는 이유가 없죠.

 

이러한 문제를 해결할 수 있는 해법으로 클립 공간(Clip Space) 라는 개념이 나오게 됩니다.

 

 

---

2. 클립 공간(Clip Space)

위에서 구한 행렬은 범용적으로 사용할 수 없기에, 범용적으로 사용할 수 있는 행렬을 만들어야 합니다. 이를 위해 사용하는 부차적인 공간이 있는데, 이것이 클립 공간(Clip Space)입니다. 뷰 공간과 NDC 공간의 중간 단계 공간이라고 보면 되고, 3차원이 모두 다 존재하는 그런 공간입니다.

 

클립 공간은 그럼 왜 3차원으로 구성되어 있을까요? NDC는 모니터 화면에 대응되는 공간으므로 2차원이면 되지 않나요? 그 해답을 알기 위해, 우선 기존 NDC 공간의 좌표 공식을 한 번 보겠습니다.

 

$$ P_{ndc}=-\frac{d}{v_z}(\frac{v_x}{a},v_y) $$

 

위 식을 보면, 모든 좌표(\(x, \ y\))를 \(v_z\) 로 나누고 있습니다. 이걸 나누기 전의 값들을 사용해 좌표를 구성해 보겠습니다.

 

$$ P_{clip} = (\frac{d \cdot v_x}{a}, \ d \cdot v_y, \ -v_z) $$

 

이렇게 구성한 다음, \(-v_z\) 로 나누면, NDC의 좌표값을 얻을 수가 있습니다.

 

$$ P_{ndc} = (-\frac{d \cdot v_x}{v_z \cdot a}, \ -\frac{d \cdot v_y}{v_z}, \ 1) $$

 

즉, 클립 공간의 값들을 점마다 각자 가지고 있는 \(-v_z\) 값으로 나누면 NDC 좌표를 얻을 수 있게 되죠. 여기에서 우리는 클립 공간을 범용적으로 활용할 수 있는 행렬로 사용할 생각을 할 수 있습니다. 이에 따라 만든 다음 행렬은 클립 공간을 만들기 위한 행렬이며, 이를 원근 투영 행렬(Perspective Projection Matrix)라고 부릅니다.

 

$$ P\cdot\ v=\left[\begin{matrix}\frac{d}{a}&0&0\\0&d&0\\0&0&-1\\\end{matrix}\right]\left[\begin{matrix}v_x\\v_y\\v_z\\\end{matrix}\right]=\left[\begin{matrix}\frac{d}{a}\cdot v_x\\d\cdot v_y\\-v_z\\\end{matrix}\right] $$

 

이 행렬을 통해 만들어진 좌표에다가 수동으로 각자의 \(-v_z\) 값을 나누어주기만 하면, 각 점에 대한 NDC 좌표를 얻을 수 있게 되는 것입니다.

 

 

동차 좌표계(Homogenous Coordinate System)

이제 조금 어려운 이야기를 해보려고 하는데, 우선 우리가 사용하는 3차원 컴퓨터 그래픽스에는 두 가지 공간이 있습니다.

• 물체를 배치하고 사용하기 위한 \(x, \ y, \ z\) 축이 서로 직교하는 현실(월드) 공간  👉🏻  유클리드 공간(Euclidean space)
• 눈(카메라)로 관찰하는 공간  👉🏻  사영 공간(Projective space)

 

사영 공간은 수학적인 용어로, 우리가 위에서 봤던 클립 공간 개념과 동일합니다. 이제 이 유클리드 공간과 사영 공간이 어떠한 차이가 존재하는지 알아볼 건데요. 우선, 유클리드 공간에서는 서로 평행한 두 직선이 만나지 않습니다.

 

유클리드 공간에서 서로 평행한 두 직선

 

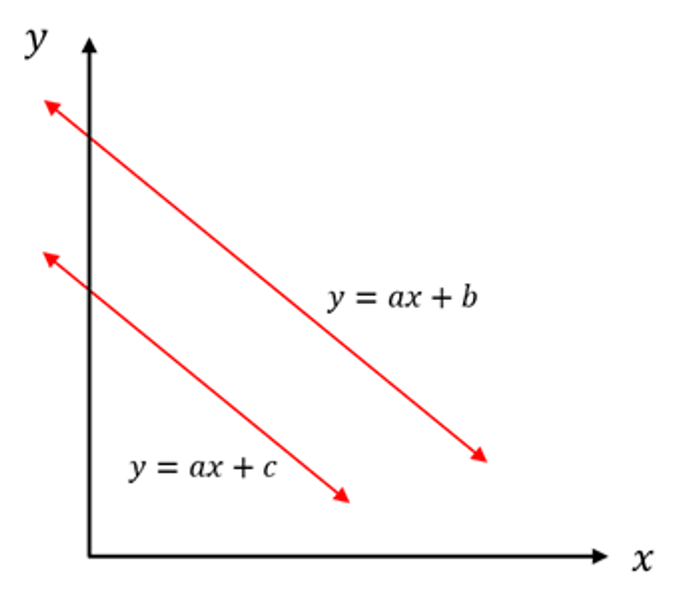
그런데, 만약 위와 같은 2차원 공간이 실은 3차원 공간의 일부였다면 어떨까요? 현재 2차원에서 보는 좌표는 3차원 공간의 일부분이었는데, 마지막 차원의 값으로 나누었다고 생각해 보는거죠.

 

$$ (x', \ y', \ z')\mapsto(x, \ y, \ 1) $$

$$ x = \frac{x'}{z'} $$

$$ y = \frac{y'}{z'} $$

 

이 개념을 적용한 직선의 방정식은 다음과 같습니다.

 

$$ y = ax + b \ \rightarrow \ \frac{y\prime}{z\prime}=a\frac{x\prime}{z\prime}+b $$

 

양 변에 \(z'\)을 곱하면 다음과 같은 식을 얻을 수 있습니다.

 

$$ y\prime=ax\prime+bz\prime $$

 

위 식을 보면, \(x\prime, \ y\prime, \ z\prime \) 모두 다 동일한 1차항 수를 가지고 있기에, 이를 동차 방정식(Homogenous Equation)이라고 부릅니다. 이 쯤 되면 느끼셨겠지만, 위 과정은 우리가 클립 공간 👉🏻 NDC 공간으로 변환하는 과정과 동일하죠.

 

$$ (zx, zy, z)\mapsto(x,y,1) $$

 

결국, 클립 공간이라는 것은 NDC 공간에서는 알 수 없는 한 차원 더 높은 공간이라는 컨셉으로 이해할 수 있겠습니다. 그럼, 클립 공간이 동작하는 원리 중 하나인 소실점(Vanishing point)에 대해 알아보겠습니다.

 

 

소실점(Vanishing point)

유클리드 공간에서는 평행한 두 직선이 절대로 만나지 않는다고 이야기 했었습니다. 그런데, 사영 공간에서는 어떨까요? 다음과 같은 식을 봤을 때, \(x, \ y\) 가 증가할 때 \(z\) 도 항샹 영향을 미친다는 것을 알 수 있습니다.

 

$$ y\prime = ax\prime + bz\prime $$

 

유클리드 공간에서는 세 축이 서로 직교하는 상태이기 때문에 \(z\) 는 \(x, \ y\) 에 전혀 영향을 미치지 않습니다. 하지만 사영 공간에서는 이 \(z\) 가 \(x, \ y\) 에 영향을 미치기 때문에, \(z\) 가 늘면 늘수록 \(x, \ y\) 값이 계속 늘어나는 성질을 가지고 있습니다.

 

 

\(z\) 값이 줄어들어 0이 되면, 다른 기울기를 가지고 있는 어떠한 선이라도 모두 0으로 수렴하게 될 겁니다. 이러한 특징 때문에 사영 공간에 속한 점들은 모두 같은 카테고리를 가진다라고도 이야기를 합니다. 서로 다른 기울기를 가진 점들이라 할 지라도 결국에는 다 원점에서 모이기 때문에 같은 종류의 점이라고 보는 겁니다.

 

 

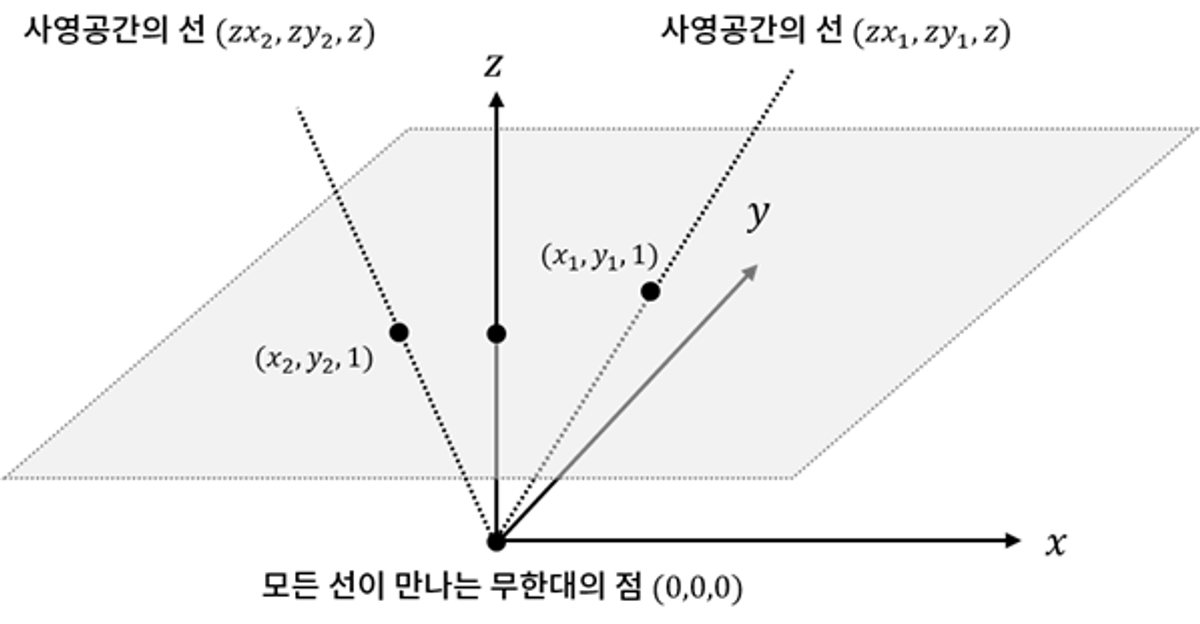
위 그림에서 \((0, \ 0, \ 0)\) 점 반대 방향에 있는 선의 경우에도, \(z\) 값이 무한대인 점에서 모인다는 이러한 원리가 사영 공간의 원리라고 할 수 있겠습니다.

 

다시 정리하자면, 마지막 차원의 요소는 항상 \(x, \ y\) 에 영향을 미치고 있고, 같은 비율로 존재하는 점들의 집합이 있을 겁니다. 그 집합들이 선을 이루는 거고, 이 선을 이루는 점들은 같은 성질을 가진다라고 표현하는 겁니다.

 

그럼 결국에는 무수히 많은 같은 성질의 점들이 사영 공간에 존재할 것인데,

 

$$ P_{clip}=(\frac{d\cdot v_x}{a},d\cdot\ v_y,-v_z) $$

 

우리가 사용하는 것은 \(z = 1\) 인 부분만 취하자는 겁니다. 이 부분이 우리가 진짜로 모니터에 출력할 때 사용할 화면이기 때문이죠. 클립 공간에서 NDC 공간으로 변환할 때, \(v_z\) 을 나누었고 \(z = 1 \) 이 되었죠?

 

$$ P_{ndc}=(-\frac{d\cdot v_x}{v_z\cdot a},-\frac{d\cdot v_y}{v_z},1) $$

 

이러한 원리를 이용해, 사영 공간에 존재하는 무수히 많은 같은 성질의 점들 중 딱 하나만 우리가 원하는 걸 뽑아볼 수 있는 겁니다. 이러한 규칙을 적용하여 화면에 점들을 그릴 때, 만약 \(v_z\) 값이 무한대가 되면 어떻게 될까요?

\(P_{ndc}\) 에서 \(x, \ y\) 는 0이 되기 때문에, \( P_{clip}\mapsto(0,0,1) \) 으로 수렴하게 될 겁니다.

 

\(v_z\) 가 무한대가 되기 때문에, 뷰 좌표계에서 \(-v_z\) 는 카메라로부터 무한대에 위치한 점이 될 겁니다. 이는 회화에서의 소실점(Vanishing point) 개념과 동일한 원리를 가지죠.

 

소실점

 

즉, \(x, \ y\) 가 0이 되기 때문에 NDC 공간에서는 중앙점 \((0, \ 0)\)이 되고, 위 그림처럼 카메라로부터 엄청 멀리 떨어진 물체들은 이 점에 가깝게 모인다라고 볼 수 있습니다. 해당 점은 NDC 좌표 (\(0, \ 0\))에 수렴한다고 말할 수 있겠네요. 이러한 소실점의 원리를 감안해, 차원에 맞춰서 원근 투영 행렬을 다음과 같이 설계할 수 있습니다.

 

$$ P=\left[\begin{matrix}\frac{d}{a}&0&0&0\\0&d&0&0\\0&0&-1&0\\0&0&0&1\\\end{matrix}\right] $$

 

마지막 차원은 사실상 의미가 없고, \(z\) 값만 마이너스로 교체해주면 됩니다. 또한, \(4 \times 4\) 행렬을 맞춰줘야 렌더링 파이프라인에 사용할 수 있게 되겠죠. 다른 이동, 회전 이런 행렬들 또한 3차원 공간에서 모두 \(4 \times 4\) 행렬이었으니까요.