2023. 11. 30. 14:48ㆍComputer Sciences/Game Mathemathics
*인프런 <게임 엔진을 지탱하는 게임수학, 이득우 교수님> 강의를 듣고 공부한 글입니다.
*여기에 나오는 예시들은 오른손 좌표계에 Y-up 체계를 기준으로 합니다.
1. 3차원 공간
왼손 좌표계와 오른손 좌표계
2차원 공간은 \(x, \ y\) 축 2개만 사용하면 간단하게 구현할 수 있었는데, 3차원 공간같은 경우에는 축(\(z\))이 하나 더 늘어나게 됩니다. 3개의 축으로 구성된 3차원 공간을 어떻게 설계하는지에 따라, 앞으로 전개할 수학식이나 응용 프로그램의 사용 방식이 달라지게 되므로, 이 체계를 확실하게 잡는 것부터 먼저 시작해야 합니다.
이러한 체계에는 왼손 좌표계와 오른손 좌표계가 있습니다. 일반적으로 모니터를 바라봤을 때, 오른쪽을 \(x\) 축, 위쪽을 \(y\) 축으로 고정해두는 편인데, 이 나머지 \(z\) 축이 모니터 안 쪽 너머로 들어가면 왼손 좌표계, 앞쪽으로 빠져나오면 오른손 좌표계입니다.

왼손 좌표계는 \(z\) 축이 모니터 너머를 향하고 있기에 배경을 관찰하는 데에 적합하고, 오른손 좌표계는 \(z\) 축이 모니터 앞면을 향하고 있기에 물체를 관찰하는 데에 적합합니다.
윗방향(Up) 축으로 무엇을 사용할 것인가?
윗방향(Up) 축은 주어진 벡터로부터 회전 행렬을 만들 때 유용하게 사용되므로, 이 축을 무엇으로 할 지 정하는 것 또한 중요합니다. 다음 사진은 우리 주변의 수많은 응용프로그램들이 왼손좌표계와 오른손 좌표계, 윗방향 축을 어떤 걸 쓰는 지에 대해 정리해 놓은 것입니다.

2. 3차원의 트랜스폼 설정
2차원에서 3차원으로 확장할 때, 이동(T)과 크기(S) 변환은 문제가 없습니다. 각 축이 서로 직교하기 때문에 차원을 추가해 해결할 수 있기 때문이죠. 하지만, 회전(R) 변환은 각 축이 서로 연관되어 있기 때문에 단순히 차원을 추가하는 방식으로는 해결할 수 없습니다. 이 내용은 추후 오일러 각을 배울 때, 자세히 알아보도록 하겠습니다.
회전의 매커니즘
강체 변환(Rigid Transformation)이란 용어를 우선 알아야 하는데, 이것은 3차원을 이루는 세 기저 벡터가 크기 변화없이 서로 직교한 상태를 그대로 유지하는 것을 말합니다. 3차원이니 \(z\) 축까지 포함된 \( 3 \times 3\) 회전 변환 행렬이 다음과 같이 구성될 겁니다.
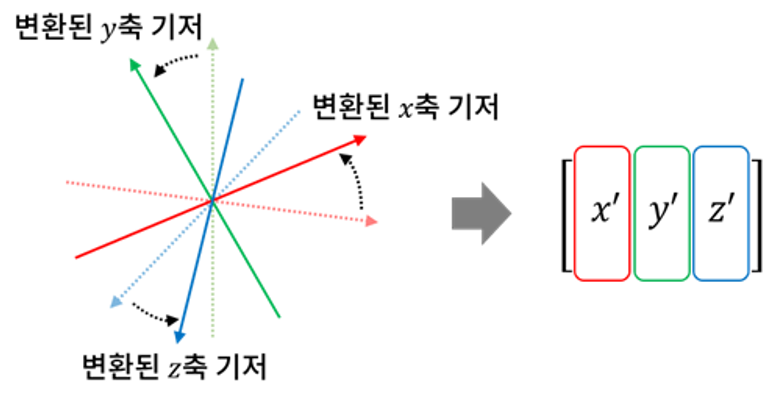
변환된 표준 기저 벡터를 각각 \(x', \ y', \ z' \) 라고 하면, 다음과 같이 표현할 수 있습니다.
$$ x' = (x'_x, \ x'_y, \ x'_z) $$
$$ y' = (y'_x, \ y'_y,, \ y'_z) $$
$$ z' = (z'_x, \ z'_y, \ y'_z) $$
이에 따라, 3차원 공간의 \(TRS\) 행렬은 다음과 같이 구성할 수 있습니다.
$$ S = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0& 0 & 1 \end{bmatrix} $$ $$ R = \begin{bmatrix} x'_x & y'_x & z'_x & 0 \\ x'_y & y'_y & z'_y & 0\\ x'_z & y'_z & z'_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
$$ T = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
따라서, 위 세 행렬의 순서에 맞게 미리 곱한 모델링 행렬 \(M\) 은 다음과 같이 구할 수 있습니다.
$$ M = T \cdot R \cdot S = \begin{bmatrix} x'_x s_x & y'_x s_y & z'_x s_z & t_x \\ x'_y s_x & y'_y s_y & z'_y s_z & t_y \\ x'_z s_x & y'_z s_y & z'_z s_z & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
3. 3차원 공간의 카메라 시스템
카메라 관점에서 월드를 바라보기
이 글 맨 위에서 Y-up 오른손 좌표계에 관한 예제로 설명한다고 했던 것과 같이, 카메라 또한 Y-up 오른손 좌표계를 사용한다고 가정해 봅시다. 해당 좌표계에서는 \(Z\) 축이 모니터 앞으로 빠져나오는 방향이므로, 월드 공간의 원점에 물체를 두면 해당 물체가 모니터를 바라보는 우리 쪽을 향하게 됩니다.
우리가 해당 물체를 관찰하려면 양의 \(z\) 방향에다가 카메라를 두고 180도 돌려야 하므로, 다음 그림과 같이 카메라와 물체가 서로 마주보는 상황을 만들게 될 겁니다.

그런데, 카메라의 \(X\) 축 방향이 물체와 달리, 오른쪽 방향이 아니라 왼쪽 방향을 가리키는 것(\(Z\) 축 앞에서 바라봤을 때)을 볼 수 있습니다. 보통 일반적으로는 화면에서 최종 결과물의 \(X\) 축은 오른쪽으로 향하기로 약속했었는데, 반대이다 보니 보는 사람이 뒤집어져서 보인다는 문제가 생깁니다.
이를 해결하려면, \(Y\) 축을 180도 회전시키면 됩니다. 즉, 카메라가 \(-Z\) 축 방향을 바라보도록 만드는 거죠.

이렇게 하면 카메라는 \(-Z\) 방향을 정면으로 바라보게 되지만, 모니터 화면의 \(X, \ ,Y\) 축은 우리에게 익숙한 데카르트 좌표계처럼 보이게 됩니다. 따라서, 카메라의 정면 방향을 구하려면 카메라 행렬의 \(Z\) 벡터에 음수를 곱해줘야 하죠.
*왼손 좌표계를 사용할 경우에는 이와 같은 별도 처리를 할 필요가 없게 됩니다.
아무튼 위와 같이 처리한 좌표계를 뷰 좌표계(View Coordinate)라고 하고, 이러한 뷰 좌표계는 카메라가 가지는 로컬 트랜스폼에서 \(X, \ Z\) 축을 반전시키는 것을 통해 구할 수 있습니다.
뷰 행렬 제작
2차원 공간에서 뷰 행렬은 카메라 트랜스폼의 역행렬을 통해 구할 수 있었습니다.
$$ V = (TR)^{\ -1} = R^{\ -1}T^{\ -1} $$
3차원에서도 동일하게 \(R\) 의 역행렬은 전치 행렬이기 때문에, 다음과 같이 구할 수 있습니다.
$$ R=\left[\begin{matrix}x_x&y_x&z_x&0\\x_y&y_y&z_y&0\\x_z&y_z&z_z&0\\0&0&0&1\\\end{matrix}\right] \ \rightarrow \ R^{-1}=\left[\begin{matrix}x_x&x_y&x_z&0\\y_x&y_y&y_z&0\\z_x&z_y&z_z&0\\0&0&0&1\\\end{matrix}\right] $$
\(T\) 의 역행렬은 그냥 왔던 길 그대로 다시 되돌아가면 되므로 다음과 같이 구성할 수 있습니다.
$$ T^{-1}=\left[\begin{matrix}1&0&0&-t_x\\0&1&0&{-t}_y\\0&0&1&{-t}_z\\0&0&0&1\\\end{matrix}\right] $$
따라서, \(R^{\ -1}T^{\ -1}\) 행렬은 다음과 같이 구할 수 있습니다.
$$ R^{-1} T^{-1}=\left[\begin{matrix}x_x&x_y&x_z&-x\cdot t\\y_x&y_y&y_z&-y\cdot t\\z_x&z_y&z_z&-z\cdot t\\0&0&0&1\\\end{matrix}\right] $$
여기에 \(X, \ Z\) 축을 반전시키면, 우리가 원하는 뷰행렬 \(V\) 를 구할 수 있습니다.
$$ V=\left[\begin{matrix}-x_x&-x_y&-x_z&x\cdot t\\y_x&y_y&y_z&-y\cdot t\\-z_x&-z_y&-z_z&z\cdot t\\0&0&0&1\\\end{matrix}\right] $$
뷰 행렬을 적용해 3차원 큐브를 표현한 결과
1. 물체의 위치를 \((0, \ 0,\ 0) \) 에 배치
2. 물체를 \(y\) 축을 중심으로 \( 45\)º, \(x\) 축을 중심으로 \(-60\)º 회전
3. 카메라의 위치를 \((0,\ 0,\ 500)\) 에 배치
4. 카메라를 \(y\) 축으로 \(180\)º 회전

'Computer Sciences > Game Mathemathics' 카테고리의 다른 글
| [게임 수학] #19 | 벡터의 외적(Cross Product) (2) | 2023.12.05 |
|---|---|
| [게임 수학] #18 | 오일러 각(Euler angle) (2) | 2023.12.04 |
| [게임 수학] #16 | 뷰 공간(View Space) (2) | 2023.11.29 |
| [게임 수학] #15 | 게임 엔진(Game Engine) (1) | 2023.11.28 |
| [게임 수학] #14 | 텍스처 매핑(Texture Mapping) (0) | 2023.11.28 |